|
|
[ resolución gráfica 1920 X 1080 ] |
|
|
[ resolución gráfica 1920 X 1080 ] |
|
|
Afrontaremos,
pues, el reto de
documentar la deslumbrante singularidad
de lo más privado de Las Meninas,
si bien, en este análisis, daremos respuesta a la convicción cabalística de su autor.
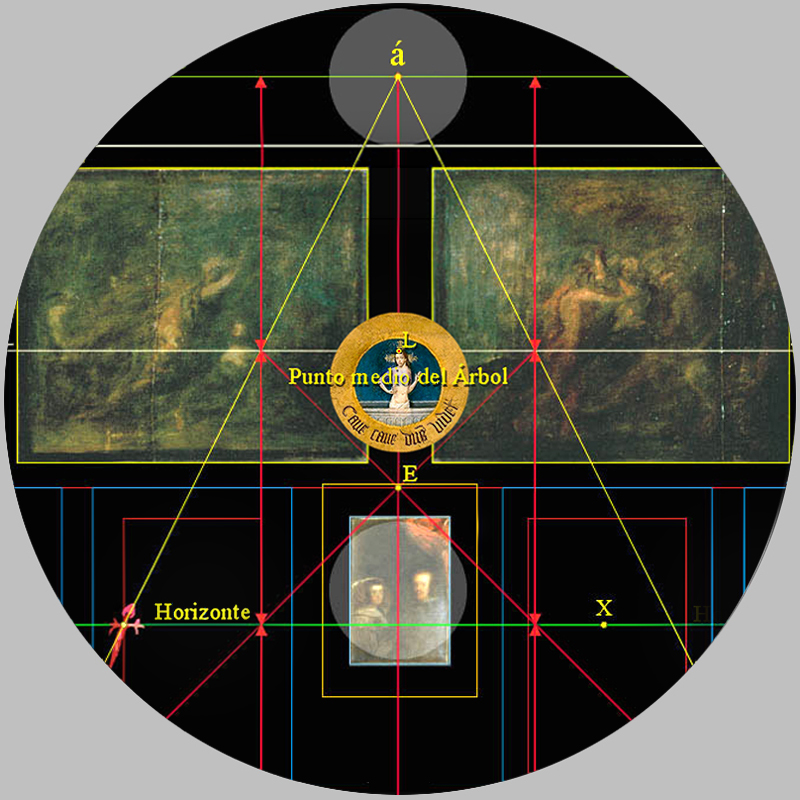
El maestro Velázquez, inmerso en su autorretrato, emplaza con exactitud el centro de la Sefira nº 8, Hod, El Honor, en la cruceta de la Cruz de Santiago, que, de acuerdo con la Kabala, es la posición designada a la esfera donde el cabalista conjura, con fe absoluta, lo que desea conseguir en el plano material.
En otras palabras:
Velázquez es huésped de las particularidades de esta Esfera.
 |
Octauum veſtimentum Dei ſeu Sephirah eſt הוד Hod, id eſt, laus, honor, gloria. Nomen eius eſt אלהים צבאות Elohim Tſebaoth; attributa eius, myſterium columnæ, ac pedis ſiniſtri, hinc trahitur ſerpens antiquus, diſciplina Domini, Ramus, Cherub, Aharon, filij regis, molæ molentes. Eſt que Canalis, per quem Deus influit in Archangelos, & per Intelligentiam Michælem in Cœlum Mercurij; Cauſa & origo animalium eſt.
La octava vestidura de Dios es la Sefira denominada el Honor, Alabanza, Gloria, es decir; Hod, cuyo nombre es אלהים צבאות, Elohim Tſebaoth. Sus atributos son: El misterio de la columna, y el pie izquierdo, de aquí surge la antigua serpiente, la disciplina del Señor, rama, querubín, Aarón, hijo del rey, muelas de molino. Este es el canal por el cual Dios fluye hacia los Arcángeles, y, a través de la Inteligencia Miguel, hacia el Cielo de Mercurio. Es la causa y el origen de los animales.
Página 294 CLASSIS IV. CABALA HEBRÆRVM - CAPVT VIII. Athanasii Kircheri. OEDIPI ÆGYPTIACI. Tomus Secundus. GYMNASIVM. ROMÆ - Anno M DC LIII |
Desconocemos, pues, las razones por la que los realistas, impresionistas, cubistas, surrealistas, informalistas, pop-arts, expresionistas, abstractos, escritores, historiadores, investigadores, arquitectos, ingenieros, médicos, poetas, autores teatrales, filósofos..., se inspiraron en tan delicado tema sin advertir lo más relevante; lo que prueba la dificultad de conocer de buena tinta el enigma que concibió su genial creador.
No obstante, el propósito del pintor quedó vinculado para siempre a su obra maestra, y en el presente se puede constatar, gracias a la textura clandestina de ciertas pinceladas, el vestigio de una extraordinaria experiencia artística.
Inequívocas pinceladas que son letras hebreas, que abren camino hacia el conocimiento de todos los misterios de la vida; la Kabala.
|
Pero la relación del lenguaje con la pintura es una relación infinita. No porque la palabra sea imperfecta y, frente a lo visible, tenga un déficit que se empeñe en vano por recuperar. Son irreductibles uno a otra; por bien que se diga lo que se ha visto, lo visto no reside jamás en lo que se dice, y por bien que se quiera ver, por medio de imágenes, de metáforas, de comparaciones, lo que se está diciendo, el lugar en el que ellas resplandecen no es el que despliega la vista, sino el que definen las sucesiones de la sintaxis.
Michel Foucault - Las palabras y las cosas. |
Al disuasorio ensayo de Michel Foucault sobre el óleo de Las Meninas le acompaña, pues, la razón de la contradicción, de manera, que, en su roll de genio, el filósofo francés aniquilaba la misma idea que le inspiró, y como antídoto, pondremos a prueba la autocrítica; aunque ahora invitamos al estudio de la convulsiva creencia que tratamos, si bien, el lector lo colmaría con honor y lealtad.
La personalidad de un individuo se puede determinar en el análisis grafológico de una simple firma, y, en este caso, será la práctica de un temerario conocimiento el que ponga al descubierto una certeza desestimada.
|
EL CONOCIMIENTO
Dahat |
 |
No hay ninguna diferencia entre lo que enseña la Kabala sobre la no-Sefira, el Conocimiento, Dahat, en el Árbol de la Vida, y el modo de Velázquez de plasmar esta misma idea en el escenario de Las Meninas con la ayuda de objetos convencionales, es decir; el pintor utilizó el recurso más seguro para ocultar a la vista de todos el velado mensaje de esta obra de arte.
Para tal empresa, elegiremos las palabras adecuadas para recuperar el mensaje de esta Pintura, y, sobre todo, considerar la particular expresión artística hebrea del pintor Velázquez que, de manera manifiesta, está en plena conformidad con la Monarquía de los Austrias.
 |
|
|
Como expresó el filósofo español José Ortega y Gasset:
|
Lo verdadero es el carácter que adquiere una proposición o creencia cuando creemos que su pensamiento coincide con la realidad; como siempre se ha dicho:
Adaequatio intellectus et rei. |
Tal y como señaló Santo Tomás en la Edad Media:
La verdad es la adecuación del intelecto con las cosas.
Summa I: 21:2
La respuesta a esta verdad estaría suscitada, pues, por la necesidad de descartar todo tipo de incertidumbre; escrita, pintada o dicha acerca de los caracteres escénicos o simbólicos de este lienzo.
 |
La lectura visual de lo que aportamos se justifica gracias a su correcto vínculo con la precisión geométrica.
Cada personaje, objeto o detalle de esta pintura, es, en particular, una imagen alegórica y activa de la cultura mágica cabalista que, lejos de ignorarse, se complementan mutuamente.
Por tanto, la interpretación de Las Meninas tiene una afinidad directa con su fuente de inspiración en tres frentes bien distintos:
|
|
|
El elemento esencial para una buena comprensión es el diálogo, y, en cada propuesta, escoger la imagen, palabra o ciencia útil para el examen de cada cuestión.
Aristóteles en el Libro Tercero de su Metafísica aclara lo que comentamos:
|
En efecto, una misma cosa puede conocerse de muchas maneras, pero los que conocen un objeto por lo que es, le conocen mejor que los que le conocen por lo que no es. |
Metafísica - Libro III - Capítulo II
El primero en establecer los
fundamentos de la Geometría plana,
una de
las ramas de la Matemática que
estudia las propiedades de superficies planas; el cuadrado, el triángulo y el
círculo, fue Euclides en el siglo III a.c. en su tratado Elementos de
Geometría.
A esta Geometría elemental también se la conoce como Geometría euclidiana.
|
La perspectiva de la pintura italiana, a diferencia de la del norte europeo basada en la observación directa de la realidad, se consolidó en la Geometría euclidiana. |
En la Geometría de Euclides las paralelas son siempre equidistantes, y, por mucho que se las prolonguen, nunca conectan en un punto, sin embargo, en la Geometría no euclidiana, producto de la experiencia visual, este postulado, como demostró Filippo Brunelleschi, 1377-1446, se revelaba falso, ya que en la práctica del dibujo todas las paralelas convergen, a la altura del horizonte, en el punto de fuga.
|
|
|
|
Fue, pues, Piero della Francesca, 1415-1492, el primer pintor del Renacimiento que utilizó una Matemática sofisticada, lo cual supuso el puente entre la perspectiva artística y la geométrica, no obstante, tras su muerte, sus investigaciones inspiró a notables autores de tratados de Geometría, como es el ejemplo, a finales del siglo XV, el libro DE DIVINA PROPORTIONE de Luca Pacioli, ilustrado por Leonardo da Vinci, donde están presentes los estudios de Piero, sobre los sólidos geométricos.
 |
|
 |
|
 |
| Fuego | Tierra | Universo | Aire | Agua |
| tetraedro | hexaedro | dodecaedro | octaedro | icosaedro |
|
De Divina Proporción de Luca Pacioli |
El título DE DIVINA PROPORTIONE hace referencia a la razón o proporción del número áureo, y, en su primera parte, trata de los polígonos y la perspectiva usada por los pintores del Quattrocento.
|
|
|
Número áureo Phi - Φ |
|
|
Para Leonardo da Vinci, como también lo fue para el alemán Alberto Durero, toda práctica pictórica debía sustentarse en la ciencia de la Matemática y Geometría.
Nicolás Copérnico, 1473-1543, en su obra titulada: Movimiento de los planetas, un libro proscrito por la ortodoxia católica, pero que se hallaba en la biblioteca personal de Velázquez, este tipo de Geometría es aplicada al estudio del orden del Cosmos.
|
|
|
|
Años más tarde, Johannes Kepler, matemático y astrónomo, expresaba en el año 1596, en su obra el MYSTERII COSMOGRAPHICI, su admiración por la proporción áurea.
El Triángulo de Kepler combina cuatro conceptos claves de Geometría y Matemática;
el Teorema de Pitágoras,
el número áureo,
la proposición 47 de los Elementos de Euclides [1]
y el Teorema de Tales de Mileto, que afirma que cualquier ángulo inscrito en un semicírculo es un ángulo recto.
Y cierto es que Velázquez, además de pintar con gran naturalismo, compuso su obra maestra con proporción áurea, una Geometría cuya utilidad se demuestra con la ayuda de un cuadrado de 152 unidades de lado.
|
Sistema de medidas |
Anchura |
|
Altura |
|
Total de Coordenadas |
|
unidades |
152 |
x |
152 |
= |
23.104 |
|
metros |
3,141333... |
x |
3,141333... |
|
|
|
|
Proponemos, pues, un triángulo Áureo cuya hipotenusa equivale al lado de la rejilla de trabajo de 152 unidades:
|
TRIÁNGULO DE KEPLER |
|
|
| AB / AT = 152 / 94 = 1,617021276... ⇔ Φ |
|
Progresión geométrica de Kepler
Y aplicando el Teorema de Pitágoras obtendríamos:
|
De manera, que el maestro español propuso la visualización del lienzo de Las Meninas a través de la progresión áurea de los tres lados del Triángulo de Kepler, y, consecuentemente, de las tres áreas cuadradas adyacentes que forman su perímetro.
|
|
|
|
En 1637 Descartes publicaba los hallazgos de la Geometría analítica usando un conjunto de ejes y coordenadas en un apéndice al Discurso del Método, un nuevo tipo de Geometría que permitía representar las rectas, curvas y figuras geométricas mediante el valor numérico de las expresiones algebraicas.
|
Cualquier punto del plano se puede localizar respecto a un par de ejes perpendiculares; dichos ejes se cortan en un punto que recibe el nombre de origen de coordenadas. |
En este mismo siglo XVII la Geometría proyectiva de Girard Desargues fundamentó, matemáticamente, los métodos de la perspectiva del Renacimiento, y con la que era posible la resolución de los problemas de la Geometría del espacio mediante operaciones efectuadas en un plano.
 |
Girard Desargues - GEOMETRÍA Y PERSPECTIVA
PREMIERE PARTIE DE LA REGLE DE LA PRATIQVE DE LA PERSPECTIVE - 1647 |
Respecto a la biblioteca de Velázquez, de algo más de 150 volúmenes, encontramos, sobretodo, temas relacionados con la Aritmética, Geometría y Arquitectura; un elocuente y particular gusto frente a lo que era común en la educación de un pintor a principio del siglo XVII [2].
Al alcance del pintor Diego Velázquez estuvieron, por tanto, varios tipos de Geometrías.
Sabemos que en su biblioteca personal dispuso de diversos ejemplares de Euclides; sin embargo, la Geometría analítica cartesiana, contemporánea al artista español, ha sido la que ha rehabilitado la posición de todos los puntos esenciales del óleo de Las Meninas.
No obstante, valoramos, pues, la erudición de Velázquez al hacer gala en Las Meninas de su grado de Maestro de Matemática, Magister Matheseos, una prueba académica que consistía en una demostración original del Teorema de Pitágoras, lo que acreditaba una sólida formación de Matemática y Geometría.

Y esto explica las innumerables demostraciones del Teorema de Pitágoras desde la Edad Media por personas de ámbitos tan diversos, como; filósofos, monjes, políticos, juristas, ingenieros o pintores como Diego Velázquez.
Estas demostraciones se clasificarían en tres grandes grupos:
Las algebraicas; donde se relacionan los lados y segmentos del triángulo.
Las geométricas; en las que se realizan comparaciones de áreas.
Las cuaterniónicas; en las que mediante vectores se representa la orientación de un objeto en un espacio tridimensional.
No obstante, ha tomado 350 años formular un plano concluyente del óleo de Las Meninas, que revelara la rigurosa gestación de la Geometría de este trabajo artístico, y permitiera reconstruir, con total precisión, la localización de cada elemento principal y necesario de esta composición.
|
|
|
|
Diego Velázquez, pues, se implicó en el estudio de la filosofía pitagórica, que quedó plasmada en su pintura naturalista a modo de un ideal, que, como mejor compendio, se manifiesta al observar sus efectos secundarios en el escenario de Las Meninas.
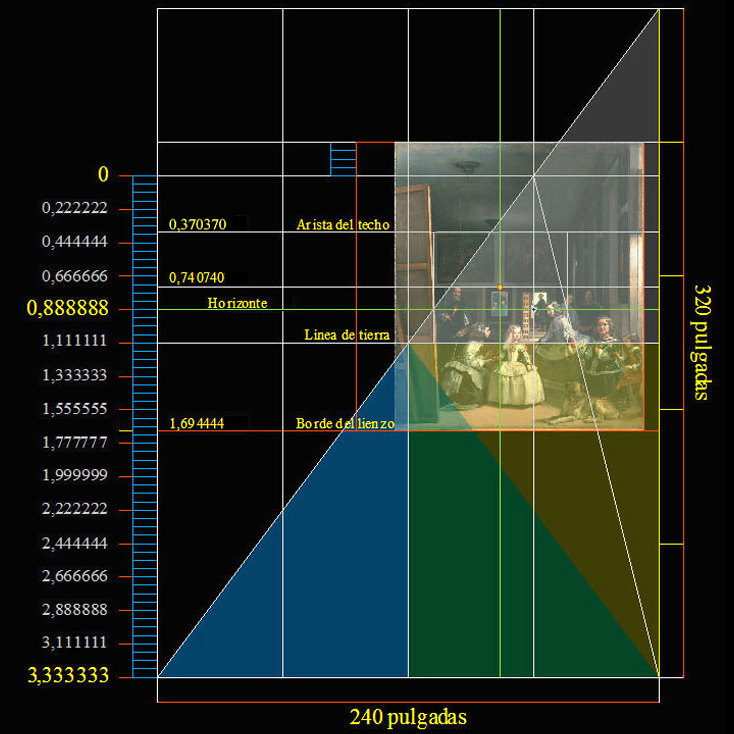
Habría que reseñar que la perspectiva que utiliza Velázquez es cercana a la de la escuela veneciana del siglo XVI, y, como se muestra en el siguiente plano basado en el Teorema de Pitágoras, se confirma gráficamente la gestación geométrica de Las Meninas, que permite escenificar, con total exactitud, la localización de cada elemento necesario y principal de esta composición.
Hablamos, pues, de la representación ideal de la Habitación del Príncipe del Alcázar de Madrid.
 |
DEMOSTRACIÓN
Luego la escala de representación de la pared del fondo será:
64 / 240 = 0,888888... / 3,333333... = 0,266666... = 1 / 3,75. |
|
|
Este plano mide físicamente 240 x 320 pulgadas, es decir; 5,58 x 7,44 metros.
| Lado del Triángulo | Cateto menor | Cateto mayor | Hipotenusa |
| Medidas en pulgadas | 80 x 3 = 240 | 80 x 4 = 320 | 80 x 5 = 400 |
| Divisiones | 60 x 4 partes | 64 x 5 partes | 100 x 4 partes |
|
|
El nombre de terna pitagórica deriva del Teorema de Pitágoras [3], y consiste en una secuencia ordenada de tres números enteros positivos; a, b y c, que cumplen con el siguiente requisito:
a² + b² = c².
|
|
|
|
| Elemento | Valor geométrico | pulgadas | metros |
| Altura total | 2 | 240 | 5,58 |
| Altura real de la Habitación del Príncipe | 1,6666 | 200 | 4,65 |
| Borde del orillo superior del lienzo | 1,1666 | 140 | 3,255 |
| Altura del punto de origen 0 | 1,0888 | 130,666 | 3,037 |
| Altura del Bastidor | 1 | 120 | 2,79 |
| Arista del techo | 0,8666 | 104 | 2,418 |
| Horizonte | 0,5 | 60 | 1,395 |
| Línea de tierra | 0,3666 | 44 | 1,023 |
| Borde del orillo inferior del lienzo | 0,0166 | 2 | 0,0465 |
| Suelo | 0 | 0 | 0 |
|
|
|
|
|
|
No obstante, nos hemos basado en dos ideas complementarias que responden a la génesis geométrica de Las Meninas:
Una la del Teorema de Tales de Mileto [4], que afirma que cualquier ángulo inscrito en un semicírculo es un ángulo recto,
y la otra compartida por dos ilustres geómetras; el Teorema de Pitágoras y la proposición 47 de Euclides.
|
|
al describe el eje vertical del punto de fuga áureo X:
al = 2 + √3/2. |
|
|
Formato de la pared del fondo
Una vez señalado el momento histórico de la infancia del
racionalismo científico, y conscientes de la importancia de su desarrollo,
operaremos con los números que deciden las medidas
exactas de la estancia del Alcázar pintada en
esta empresa velazqueña.
El análisis geométrico de la medidas exactas de la pared del fondo pintada en este lienzo se llevaría a cabo a través del siguiente método:
La anchura de la pared del fondo mide 72 unidades
Factorización de 2 x 2 x 2 x 3 x 3 = 72.
Los divisores del número 72 son 12:
1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72.
La altura de la pared del fondo mide 60 unidades
Factorización de 2 x 2 x 3 x 5 = 60.
Los divisores del número 60 son 12:
1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
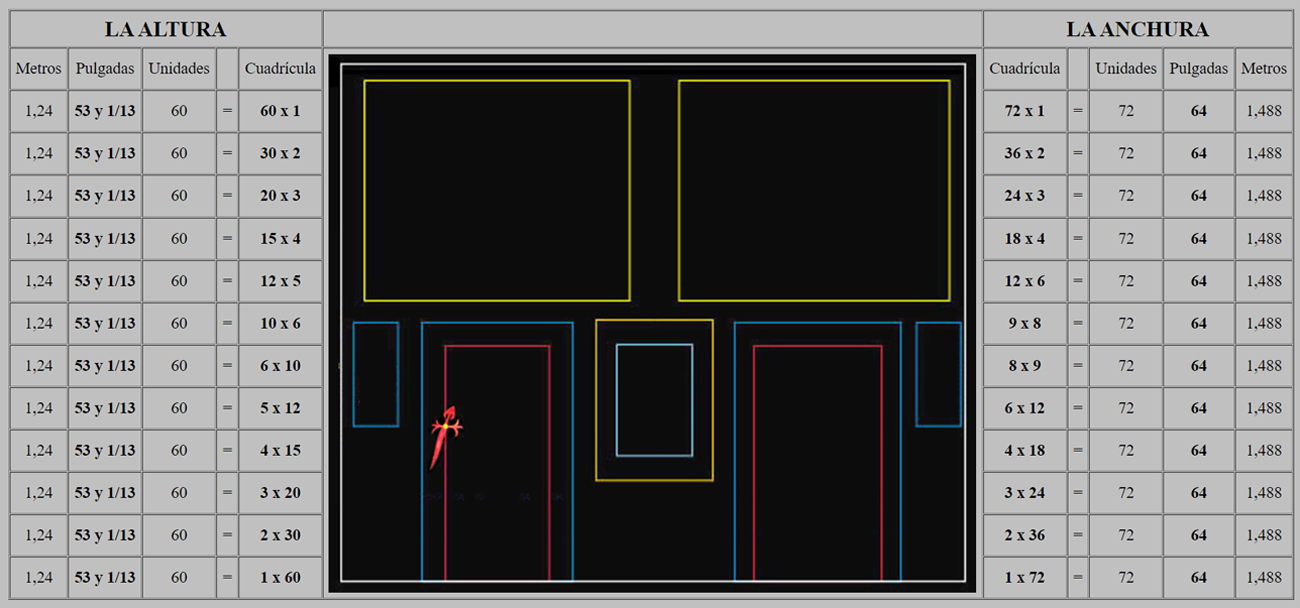 |
|
|
| Pared del Fondo | Metros | Pulgadas | Unidades | Unidades por pulgada | Tamaño real en pulgadas | |||
| Anchura | 1,488 | 64 | 72 | = | 0,3 | x | 240 | |
| Altura | 1,24 | 53 y 1/3 | 60 | = | 0,3 | x | 200 |
|
|
De donde se deduce, pues, que el espacio pictórico de Las Meninas está dominado por el número, aun cuando no se nos muestre evidente, sin embargo, sí es demostrable gracias a la siguiente comprobación:
FORMATO 8
| Formato | Proporción | Pulgadas por unidad | La anchura | Anchura en Pulgadas | Tamaño en metros | |||
| 8 | 9/8 | = | 0,888888 | x | 72 unidades | = | 64 pulgadas | 8 x 8 x 0,02325 = 1,488 metros |
La anchura de la pared del fondo pintada en el lienzo de Las Meninas mide 1,488 metros
| Formato | Proporción | Pulgadas por unidad | La altura | Altura en Pulgadas | Tamaño en metros | |||
| 8 | 9/8 | = | 0,888888 | x | 60 unidades | = | 53 pulgadas y 1/3 | 8 x 6,666... x 0,02325 = 1,24 metros |
La altura de la pared del fondo pintada en el lienzo de Las Meninas mide 1,24 metros
La pulgada castellana equivale a 0,02325 metros.
En este primer paso hemos asegurado el tamaño de la pared del fondo pintada en el lienzo de Las Meninas, aunque aún necesitaremos de un segundo procedimiento más para adentrarnos en la realidad física de esta gran sala del Palacio Real.
Formato de la Habitación del Príncipe
FORMATO 30
| Formato | Proporción | Pulgadas por unidad | La anchura | Anchura en Pulgadas | Tamaño en metros | |||
| 30 | 9/30 | = | 3,333333 | x | 72 unidades | = | 240 pulgadas | 30 x 8 x 0,02325 = 5,58 metros |
|
|
| Formato | Proporción | Pulgadas por unidad | La altura | Altura en Pulgadas | Tamaño en metros | |||
| 30 | 9/30 | = | 3,333333 | x | 60 unidades | = | 200 pulgadas | 30 x 6,666... x 0,02325 = 4,65 metros |
|
|
 |
La anchura
Tamaño en unidades: 1,125 unidades por pulgada x 64 pulgadas = 72 unidades
La altura
Tamaño en unidades: 1,125 unidades por pulgada x 53 pulgadas y 1/3 = 60 unidades
El ratio
Y estos números se convierten en la razón geométrica de su cociente:
240 / 72 = 200/ 60 = 10 / 3 = 3,333333... pulgadas por unidad |
|
|
Hemos demostrado que el tamaño real de la pared del fondo
pintada en Las Meninas depende de la proporción; para lo cual, hemos desarrollado una herramienta de medir distancias,
lo más cercano a la realidad, desde el punto de
vista del observador.
En las siguientes operaciones se determina, de manera directa, el tamaño real de la anchura y altura de la Habitación del Príncipe del Alcázar de Madrid:
|
 |
| Zona izquierda 132 pulgadas | Zona central 64 pulgadas | Zona derecha 44 pulgadas | ||
| 44 | 44 | 44 | 2 x 32 = 64 | 44 |
|
Total - 240 pulgadas |
||||
Desglose de la anchura de la Habitación del Príncipe
Y se entiende, que el ancho de fabricación de las tres telas que componen el lienzo de Las Meninas medían, respectivamente; 32 + 44 + 44 = 120 pulgadas, es decir; tres cantidades que son también partes modulares del tamaño real de la Habitación del Príncipe.
Este análisis geométrico no es
convencional, sino rigurosamente exacto, y prueba que la posición del pintor ante su
lienzo ha sido resuelta con total grado de coherencia Matemática.
|
|
|
|
Este océano de números infinitesimales, números que se pueden definir como cantidades infinitamente pequeñas, trae a la memoria que el valor: 1,111111... correspondiente al intervalo de la Línea de tierra, y equivalente a la posición de la arista inferior de la pared del fondo de Las Meninas, se halla asociado, desde hace 2500 años, a la solución matemática del argumento de Aquiles y la tortuga de Zenón de Elea [5].
|
Aquiles, uno de los principales protagonistas de la Ilíada, a quien Homero apoda el de los pies ligeros, πόδας ὠκύς, pedibus celer, decide salir a competir en una carrera contra una tortuga. Ya que corre mucho más rápido que ella, y seguro de sus posibilidades, le da una gran ventaja inicial. Al darse la salida, Aquiles recorre en poco tiempo la distancia que los separaba inicialmente, pero al llegar allí descubre que la tortuga ya no está, sino que ha avanzado, más lentamente, un pequeño trecho. Sin desanimarse, sigue corriendo, pero al llegar de nuevo donde estaba la tortuga ésta ha avanzado un poco más. |
De modo, que Aquiles no ganará la carrera, ya que la tortuga siempre estará por delante de él.
Numéricamente, la longitud que recorre Aquiles persiguiendo a la tortuga es la siguiente:
1 + 1/10 + 1/100 + 1/1000 + ...
La suma, o sea, la distancia total recorrida por Aquiles sería: 1,111111...
Los razonamientos de Zenón constituyen el testimonio más antiguo que se conserva del pensamiento infinitesimal, y, siglos más tarde, desarrollado por Leibniz y Newton en la aplicación del cálculo infinitesimal en 1666.
Del mismo modo que Zenón defendió la doctrina de su maestro Parménides, ponemos de manifiesto que la apariencia es sensible de ser engañosa; y que, ante todo tipo de incertidumbre; escrita, pintada o dicha acerca de los caracteres escénicos o simbólicos de este lienzo, debemos fiarnos únicamente de la razón para evitar la reductio ad absurdum [6].
 |
|
|
Análisis en la Cuadrícula de trabajo de la cuantía 0,111111... = 1/9.
El valor geométrico de 1/9 es de 9 unidades, que corresponden a 9 unidades / 1,125 unidades por pulgada = 8 pulgadas.
8 pulgadas x 0.02325 metros por pulgada = 0,186 metros.
La altura de la Puerta mide 30 unidades / 1,125 unidades por pulgada = 26,666666... pulgadas.
Por tanto: 26,666666... pulgadas x 0,02325 metros por pulgada = 0,62 metros, que es lo que mide la altura de esta Puerta pintada en Las Meninas.
El lado de las pequeñas celdillas cuadradas de esta rejilla mide 9 unidades / 18 celdillas = 0,5 unidades.
0,5 unidades / 1,125 unidades por pulgada = 0,444444... pulgadas = 4/9 de pulgada,
y en metros: 0,444444... pulgadas x 0,02325 metros por pulgada = 0,010333... metros.
Es decir: 9 unidades equivalen a 18 celdillas cuadradas de 1,033333... centímetros de lado.
Y a -30 unidades se sitúa, sobre la Línea de tierra, la marca del intervalo nº 5 de la altura total de la Puerta.
La anchura de la Puerta mide 18,9 unidades
Factorización de 3 x 3 x 3 x 7 = 189.
Los divisores del número 189 son 8:
1, 3, 7, 9, 21, 27, 63, 189.
La altura de la Puerta mide 30 unidades
Factorización de 2 x 3 x 5 = 30.
Los divisores del número 30 son 8:
1, 2, 3, 5, 6, 10, 15, 30.
| LA ALTURA | LA ANCHURA | |||||||||
| Metros | Pulgadas | Unidades | Cuadrícula |
 |
Cuadrícula | Unidades | Pulgadas | Metros | ||
| 0,62 | 26 y 10/15 | 30 | = | 30 x 1 | 18,9 x 1 | = | 18,9 | 16 y 12/15 | 0.3906 | |
| 0,62 | 26 y 10/15 | 30 | = | 15 x 2 | 6,3 x 3 | = | 18,9 | 16 y 12/15 | 0.3906 | |
| 0,62 | 26 y 10/15 | 30 | = | 10 x 3 | 2,7 x 7 | = | 18,9 | 16 y 12/15 | 0.3906 | |
| 0,62 | 26 y 10/15 | 30 | = | 6 x 5 | 2,1 x 9 | = | 18,9 | 16 y 12/15 | 0.3906 | |
| 0,62 | 26 y 10/15 | 30 | = | 5 x 6 | 0,9 x 21 | = | 18,9 | 16 y 12/15 | 0.3906 | |
| 0,62 | 26 y 10/15 | 30 | = | 3 x 10 | 0,7 x 27 | = | 18,9 | 16 y 12/15 | 0.3906 | |
| 0,62 | 26 y 10/15 | 30 | = | 2 x 15 | 0,3 x 63 | = | 18,9 | 16 y 12/15 | 0.3906 | |
| 0,62 | 26 y 10/15 | 30 | = | 1 x 30 | 0,1 x 189 | = | 18,9 | 16 y 12/15 | 0.3906 | |
|
|
La profundidad de Las
Meninas es matemática, y
depende de la Geometría del espacio, un
espacio que se puede representar con cifras en una cuadrícula
de ayuda superpuesta al lienzo.
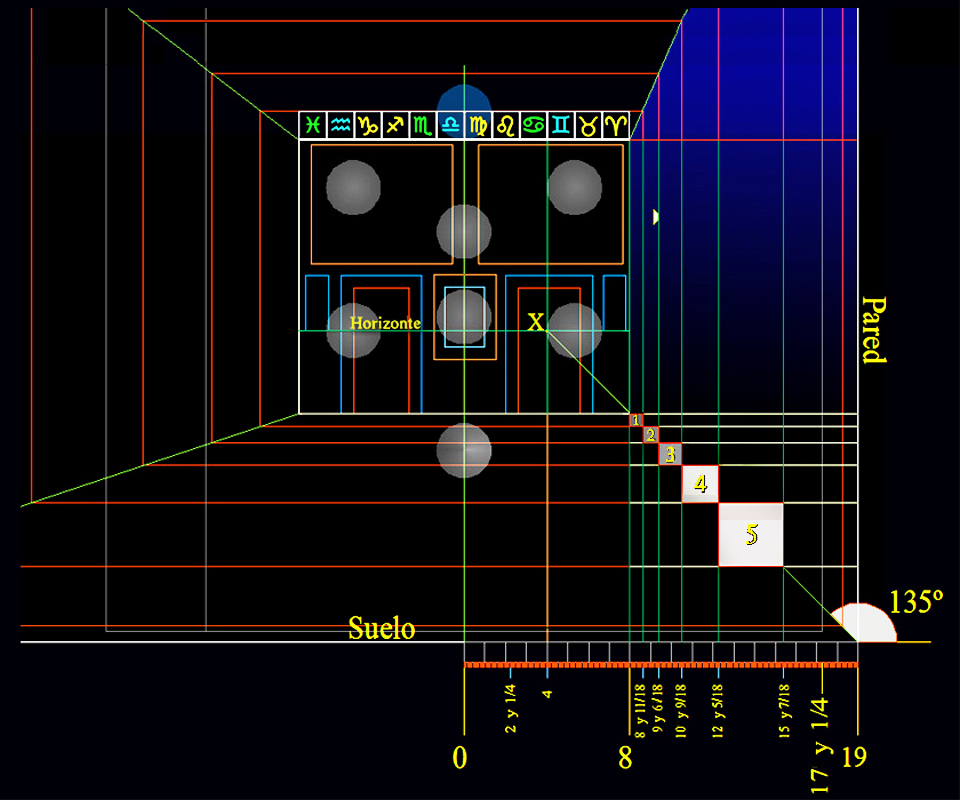
En el caso específico de la perspectiva del muro sur de la Habitación del Príncipe, la clave ha sido redescubrir un espacio aéreo diagonal de cinco planos visuales degradados, y definidos por un único punto de fuga, el punto X.
En el punto de fuga X: [18, -12], Velázquez sitúa la coordenada fija más importante del espacio físico que se representa en Las Meninas.
|
|
|
|
Esta Geometría pitagórica de Las Meninas confirma, pues, que la profundidad escalonada de los cinco distintos planos de la pared derecha están resueltos de manera segura.
|
Intervalo |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
Unidades |
2,75 |
|
3,5 |
|
5 |
|
8 |
|
14 |
|
Pulgadas |
2 pulgadas y 4/9 |
|
3 pulgadas y 1/9 |
|
4 pulgadas y 4/9 |
|
7 pulgadas y 1/9 |
|
12 pulgadas y 4/9 |
|
Incremento |
|
+ 0,75 |
|
+ 1,5 |
|
+ 3 |
|
+ 6 |
|
|
Progresión |
|
0,75 x 20 |
|
0,75 x 21 |
|
0,75 x 22 |
|
0,75 x 23 |
|
|
|
 |
|
|
Ya que recuperamos del olvido una propuesta del manual velazqueño, entendemos que éstos son los números que avalan cualquier operación matemática o geométrica sobre, fuera y dentro, del plano de Las Meninas.
En el escenario de Las
Meninas analizaremos, pues, un hallazgo que atañe al arte más privado del pintor Velázquez,
y que responde a una manera de pensar que
quedó atesorada en la sublime Geometría Sagrada de este lienzo.
Caso A - Deducción del punto medio del Árbol Sagrado:
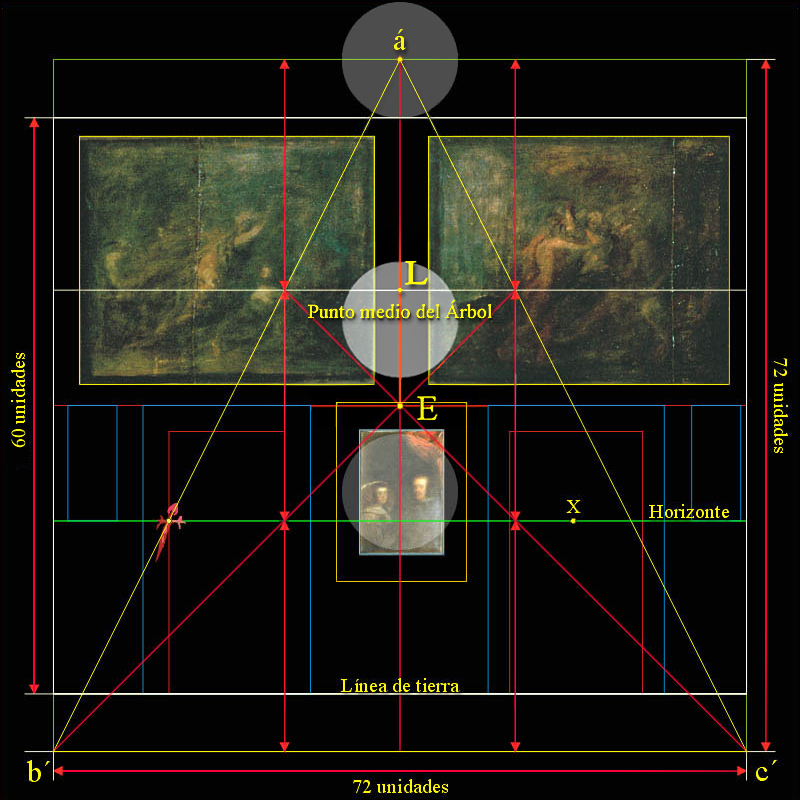 |
|
|
Y averiguado el tamaño exacto de la Habitación del Príncipe del Alcázar de Madrid, a continuación analizaremos en la rejilla de trabajo las distintas relaciones entre la pared del fondo y la motivación cabalística de Las Meninas, de modo, que la elección concreta del formato de la pared del fondo responde, pues, a la fase en que Velázquez adapta en esta pared lejana dos cuestiones complementarias:
|
| celdillas | pulgadas | Tamaño real de la pared del fondo | medidas castellanas | metros | ||
| Altura | 9/filas | 22,222... x 9 | = | 60 unidades x 3,333... pulgadas por unidad = 200 pulgadas | 200 / 36 = 16 pies y 2/3 | 4,65 |
| Anchura | 8/columnas | 30 x 8 | = | 72 unidades x 3,333... pulgadas por unidad = 240 pulgadas | 240 / 12 = 20 pies | 5,58 |
El número 72 nos lleva, pues, al Schemhamphoras, o nombre dividido, número que corresponde al conocimiento de la palabra secreta del verdadero nombre de Dios.
|
|
|
|
Escribió Platón en su libro La República:
|
(...) Creo que sabes que quienes se ocupan de geometría, aritmética y otros estudios similares dan por supuesto los números impares y pares, las figuras, tres clases de ángulos y otras cosas emparentadas con éstas y distintas en cada caso; las adoptan como hipótesis, procediendo igual que si las conocieran, y no se creen ya en el deber de dar ninguna explicación a ellos mismos ni a los demás, con respecto a lo que consideran como evidentes para todos, y de ahí es de donde parten las sucesivas y consecuentes deducciones que les llevan, finalmente, a aquello cuya investigación se proponían.
- Sé perfectamente todo esto - dijo. |
|
- ¿Y no sabes también que se sirven de formas visibles acerca de las cuales estudian, pero no pensando en ellas mismas, sino en aquello a que ellas se parecen, estudiando, por ejemplo, acerca del cuadrado en sí y de su diagonal, pero no la imagen de ellos que dibujan (...) en su deseo de ver aquellas cosas que sólo pueden ser contempladas sino por medio de la mente?
- Tienes razón - dijo. |
La República - Libro VI - apartado XX
|
|
|
|
Claro está, Platón se refería aquellas cosas o realidades del mundo metafísico; ideas o formas que sólo pueden ser percibidas por la razón pura; por lo que tal vez éste fuera el motivo de rotular a la entrada de la Academia esta significativa frase:
Nemo huc geometriae expers ingrediatur.
No entres aquí si no eres geómetra.
Para Platón los números son los ladrillos del edificio que gobiernan al mundo.
En la época de Velázquez al conjunto de las cuatro artes liberales de la antigua Grecia y del mundo medieval sobre números se denominaba el quadrivium, o cuadrivio, siendo, en verdad, pródiga la lista de esta materia en la biblioteca del pintor.
El quadrivium constaba de Aritmética, Geometría, Astronomía, o Astrología, y Música.
Ciencias de un mismo patrón teórico que han permanecido lejos de su aplicación, y posterior desarrollo, en la metódica investigación de la obra del pintor sevillano.
|
|
|
|
LA GEOMETRÍA
|
Eſta ciencia tiene mas loa que las otras tres, comprehendidas en el numero de Matematicas; porque auiendo grandes contiendas entre las ſestas de caſi todas las diſciplinas, todos los geometras en toda parte concuerdan en vno, ni jamas ſobre la facultad ſe halla entre ellos algun debate, porque aunque diſputan de los puntos, de las lineas, y de las ſuperficies, ſi ſe pueden diuidir o no; en lo demas concuerdan, ni difieren en dotrina o preceptos; antes ſe esfuerçan para exceder el vno al otro, con nueuas y mas ſutiles inuenciones.
Página 86 - DISCVRSO XCIIII. DE LOS ARQUITECTOS EN vniverſal, Fortificadores de Fuerças, y maeſtros de maquinas, o Ingenieros. Plaza Vniuersal de todas Ciencias y Artes - Christoval Suarez de Figueroa - Madrid. 1615. |
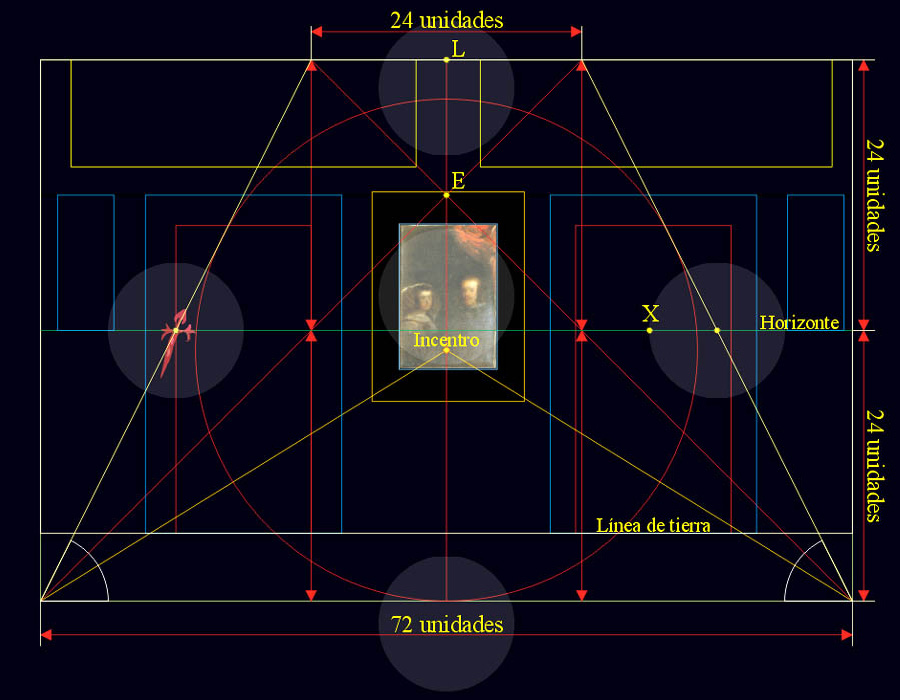 |
|
Las tres bisectrices del gran triángulo inscrito en la pared del fondo se cortan en un punto de intersección llamado Incentro, y tiene la propiedad de ser tangente a sus tres lados. |
Pitágoras es históricamente conocido como la piedra angular de la Geometría científica, y ya en el siglo VI a.c. demostró:
|
Que de las diversas leyes arbitrarias e inconexas de la Geometría empírica se puede deducir conclusiones lógicas de un número limitado de axiomas, o postulados. |
Las conclusiones geométricas de Pitágoras fueron consideradas por sus discípulos verdades evidentes, lo cual supuso una primera propuesta de cómo llamar ciencia al conocimiento:
|
Un saber que una cosa es así y no puede ser de otra manera, tal y como se enuncia incuestionable la cuarta definición del Libro I de Los Elementos de Euclides [7];
por dos puntos diferentes pasa una sola línea recta.
|
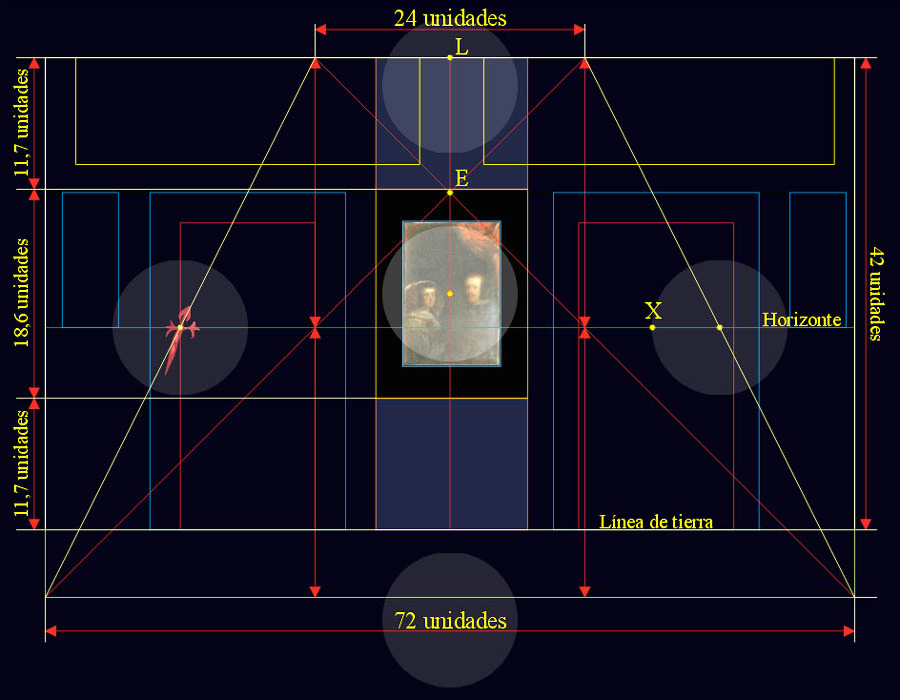 |
|
Tamaño real en la pared del fondo
|
Y será LA GEOMETRÍA AXIOMÁTICA de Euclides, que auxiliada de la regla y compás, la que sistematice el estudio de las propiedades de las figuras geométricas del modo siguiente:
Definiciones
Axiomas
Postulados
Teoremas
Después de todo, es gracias a su traducción del árabe al latín cómo fue conocida la Geometría griega en Europa; un esfuerzo que recayó en los eruditos judíos de la escuela de traductores de Toledo, ya que dominaban ambas lenguas por igual.
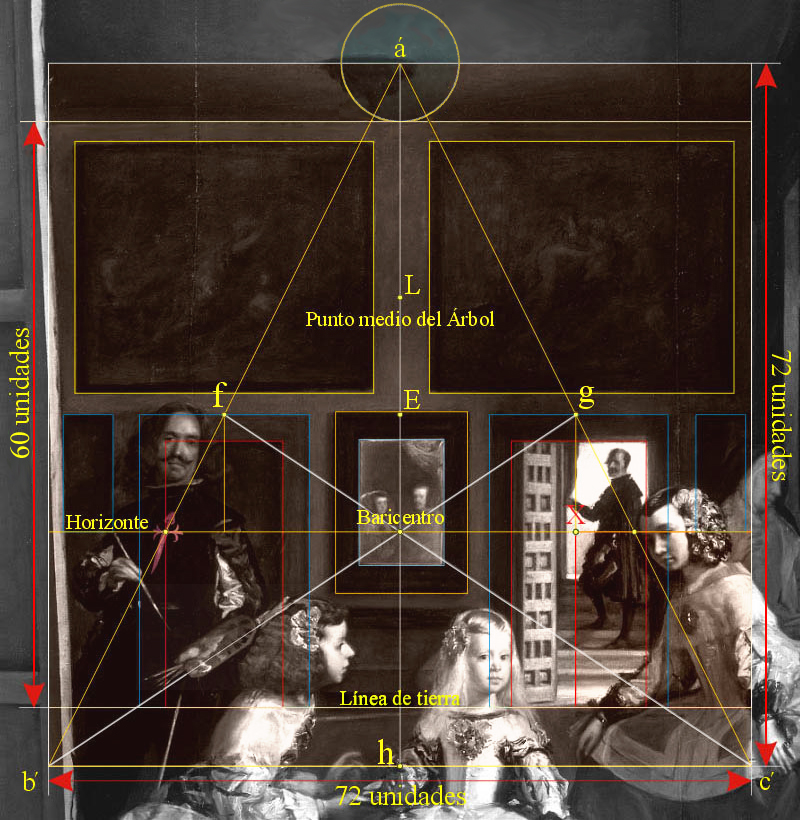 |
El Baricentro
Intersección de las tres medianas del gran triángulo.
El Baricentro se localiza en el Horizonte o nivel de ojos. |
En cuanto a los Elementos de Euclides de finales del siglo XIV, eran todavía traducciones del siglo IX de la versión árabe de los Elementos de Al-Ḥajjāj ibn Yūsuf ibn Maṭar, como es el caso de los textos de Abelardo de Bath, Herman de Carinthia o Gerardo de Cremona [8].
Velázquez, autor de tan prodigioso equilibrio y
simetría, nos ha invitado a entrar en su obra maestra, si bien,
necesitaremos más que ayuda para no caer rendidos ante las propiedades extraordinarias de su ingenioso montaje artístico.
La viabilidad de las esferas cabalísticas condicionó desde el principio la disposición del escenario de Las Meninas, ya que fueron urdidas para dar nombre y sentido al relato de zonas muy concretas.
|
|
|
|
|
|
La raíz cuadrada de 5 que es igual a 2,236, con una exactitud de casi el 100%, aparece en la fórmula del número áureo, y corresponde al tamaño de la hipotenusa de un triángulo rectángulo cuyos catetos miden 1 y 2 respectivamente.
|
Número áureo Phi - Φ |
Tenemos que 152 unidades es el tamaño del lado de la cuadrícula, que equivale a 4, y que medio lado de cuadrícula valdrá 152 ÷ 2 = 76 unidades, de lo que se deduce, que si la Sefira nº 6, Tiferet, La Belleza, se sitúa en la coordenada [0, 9], entonces, su centro estaría situado a 85 unidades del borde inferior.
|
RESOLUCIÓN
Si a 76 unidades le corresponde 2 en la cuadrícula,
entonces a 85 unidades le corresponderá X:
X = 85 x 2 ÷ 76 = 2,236... ⇔ √5, que es el resultado que buscamos. |
LA CUADRATURA DEL CÍRCULO
|
|
|
|
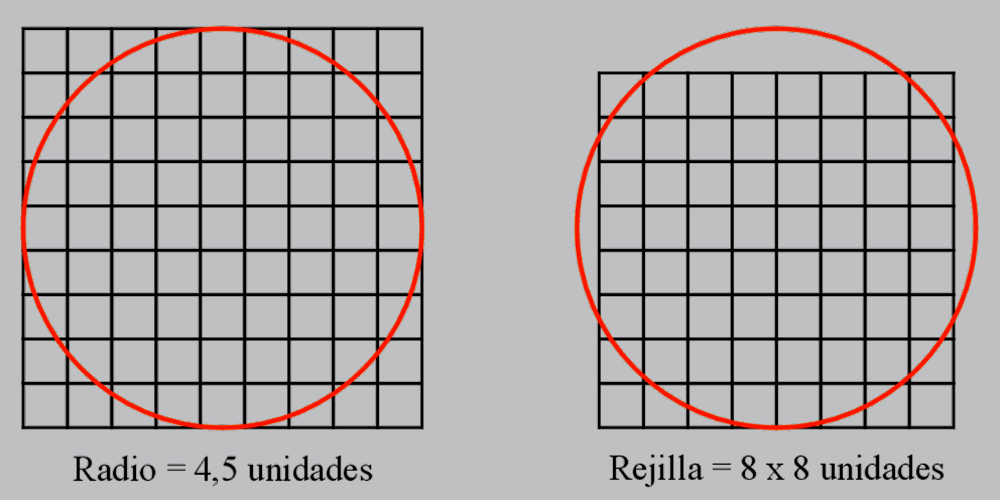
La gran cuadrícula de 64 subcuadrados se haya relacionada, pues, con uno de los problemas más conocido de la Matemática, la cuadratura del círculo, un acertijo que consiste en obtener un Cuadrado que tenga la misma área que un Círculo; y aunque este problema geométrico no tuvo solución exacta durante siglos, si bien, en las antiguas culturas de oriente si hubo intentos empíricos para su cálculo.
 |
|
|
En el Papiro de Ahmes de 1650 a. c. se encuentra un procedimiento que utiliza el diámetro de un círculo dividido en 9 partes.
El escriba Ahmes calcula el área del círculo con un valor de Pi = 256/81 = 3,1605..., y un diámetro igual al lado de 9 unidades del cuadrado circunscrito.
|
OPERACIÓN
π × 4,52
3,1605... × 4,5 × 4,5 = 64 unidades cuadradas |
Y se comprueba, pues, que 64 unidades cuadradas del área del círculo equivalen a una cuadrícula de 8 x 8 unidades, lo que prueba que la cuadratura del círculo no era una misión imposible hace 3600 años.
Velázquez, por tanto, afronta la Cuadratura del Círculo en Las Meninas, y, propone, con la ayuda de una cuadrícula de 8 x 8, que denominamos Límite de la rejilla de 152 unidades, la estructura del espacio aéreo de las esferas cabalísticas denominadas los 10 Sefirot.
Hablamos de una gran cuadrícula de 64 subcuadrados, que vienen a ser el mismo número de casillas que componen el tablero del juego del Ajedrez.
Veamos, pues, cómo se gestiona en este lienzo la cuadratura del círculo:
|
Área del Cuadrado; 4 × 4 = 16
Área del Círculo; π × (√5)2 = 15,707... |
La Cuadratura del Círculo en Las Meninas, con el Pi de Arquímedes 22/7 = 3,14285714286..., corresponde al 98,214... %
Estas muestras del buen hacer velazqueño, y las conclusiones que aporta este análisis son definitivas, y, ya que no es posible descubrir todo al mismo tiempo, para mayor control, sería oportuno tener bien presente la coordenada: [0, 12], que es, pues, donde se halla el punto medio del Árbol Sagrado.
|
|
Espacio geométrico de la Sefira VI - Tiferet - La Belleza.
Sello Divino
Emet Adonai - Verdad de Dios |
En el Corazón del Árbol, en la Sefira nº 6, Tiferet, La Belleza, que se sitúa en la pared del fondo encima del espejo, es donde la presencia divina, o Shekinah, שכינה, se manifiesta, y alude, pues, al lugar exclusivo de la morada de Dios en el Templo de Jerusalén.
|
|
|
Athanasius Kircher - Roma - 1652 |
El uso de los Sefirot [9], nombre con el que se conoce a las diez esferas del Árbol Sagrado, es materia de trabajo del cabalista, y su manipulación requiere de fórmulas que deben ser conocidas de memoria.
El cabalista se emplaza de manera voluntaria en el espacio de la Sefira Hod.
Hod, El Honor, la octava Sefira, es la dueña soberana de la esfera de la Magia, y de la dinámica creatividad del planeta Mercurio.
Caso B - Deducción del punto medio del Árbol Sagrado:
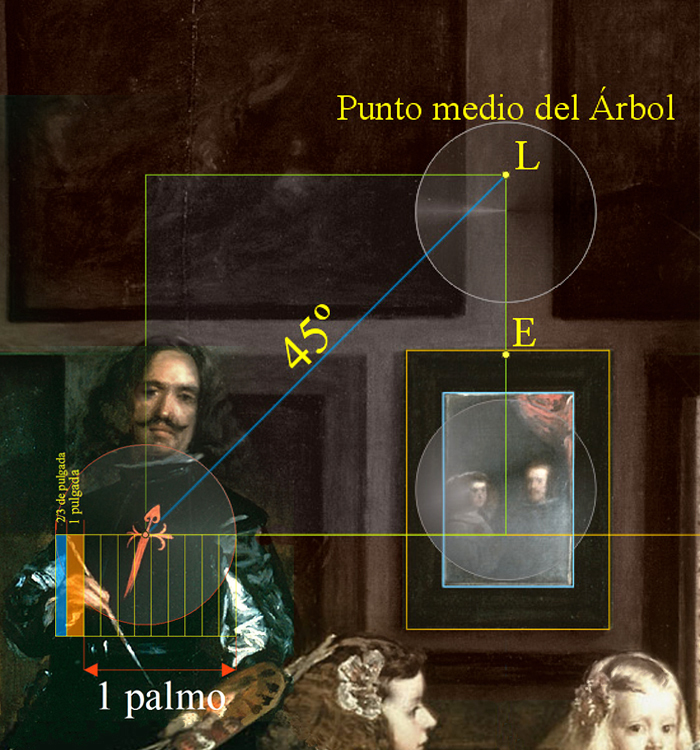 |
Si trazamos un vector, con una inclinación de 45º, desde la cruceta del Hábito de la Cruz de Santiago hasta el pilar Central del Árbol Sagrado, encontraremos su punto medio, el punto L, que tiene por coordenada: [0, 12].
En Las Meninas el punto E es el centro de coordenadas; [0, 0]. |
En la lectura de un nivel superior, en la esfera nº 6, denominada Sefira Tiferet, La Belleza, hallamos el punto medio del Árbol Sagrado, y que, a través de un vector trazado con un ángulo de 45º, conecta con la propia cruceta de la Cruz del Hábito de Santiago situada en el mismo corazón del pintor, y que es centro, a su vez, de la Sefira nº 8, Hod, El Honor.
Observamos, pues, la muy pensada posición de la cruceta de la Cruz del Hábito de Santiago, que alojada en el pecho del pintor, ratifica, desde el leb, לב, corazón, la formulada convicción cabalística.
| letra latina |
letra hebrea |
signo |
valor numérico |
Total |
| L |
Lamed |
|
30 |
32 |
| B |
Bet |
|
2 |
Es decir; לב se lee leb, y se traduce por corazón, pero, lo que es más importante; son la última y primera letra de la Torah, por lo que dicha palabra encierra la totalidad de la revelación escrita desde el principio de Israel:
En el principio... Israel.
Bereshit... Israel.
 |
Y recordaríamos que el Sefer Yetzirah también comienza con la letra Bet, y que en su primer renglón se habla del número 32.
|
Numeración |
Sefira |
Castellano |
בשלשים ושתים נתיבות פליאות חכמה חקק יה יהוה צבאות אלהי ישראל אלהים חיים ומלך עולם אל שדי רחום וחנון רם ונשא שוכן עד וקדוש שמו מרום וקדוש הוא וברא את עולמו בשלשה ספרים בספר וספר וספור׃
Con treinta y dos senderos prodigiosos de Sabiduría grabó Yah, el Señor de los Ejércitos, el Dios de Israel, Elohim vivo, Rey del mundo, El Shaddai Misericordioso y Clemente, Elevado y Supremo, que reside en la Eternidad y su nombre es Santo.
Y creó Su mundo con tres libros:
Sefer Yetzirah 1:1 |
||
|
I |
Kether |
וקדוש |
Santo | ||
|
II |
Chokmah |
ונשא |
Supremo | ||
|
III |
Binah |
רם |
Elevado | ||
|
Dahat |
עד |
Eternidad | |||
|
IV |
Chesed |
וחנון |
Clemente | ||
|
V |
Geburah |
רחום |
Misericordioso | ||
|
VI |
Tiferet |
אל שדי |
El Shaddai | ||
|
VII |
Netzach |
ומלך עולם |
Rey del mundo | ||
|
VIII |
Hod |
אלהים חיים |
Elohim vivo | ||
|
IX |
Yesod |
אלהי ישראל |
Dios de Israel | ||
|
X |
Malkhut |
יהוה צבאות |
Señor de los Ejércitos | ||
|
|
De acuerdo con la Kabala cristiana, la Sefira Tiferet se haya relacionada con la resurrección de Jesucristo en el Santo Sepulcro y el arcángel Rafael [10].
|
Jeroen van Aeken - El Bosco - Jerónimo Bosch. 1450 - 1516
Museo del Prado - Madrid |
Athanasius Kircher, sacerdote jesuita, políglota, erudito, estudioso orientalista, de espíritu enciclopédico y uno de los científicos más importante del siglo XVII, añade en latín los siguientes contenidos:
|
6 תפאר Tiphereth, Pulchritudo.
|
Sexta Sephirah ſeu veſtimentum Dei תפארת Tiphereth dicitur, cuis nomen יהוה Iehoua; Attributa eius ſunt ſpeculatio illuminans, lignum vitæ, voluptas, linea media, linea viridis, ambiens vniuerſum, lex ſcripta, Sacerdos magnus, ortus ſolis, ſpecies purpurea, ſeptuaginta duæ nationes in terra, ſigillum eius אמת אדני ; myſterium que eius in tertia litera tetragrammati, homo ſupremus ſiue Adam Cœleſtis, arbor in medio Paradiſi plantata. Per hanc Deus influit in ordinem virtutum, & hinc per Intelligentiam Raphael in Sphœram ſolis. Cauſa eſt omnis harmoniæ & pulchritudinis, quam in vniuerſso intuemur. |
|
|
|
|
|
|
|
6 תפאר Tiferet, Belleza.
|
La sexta vestidura de Dios es la Sefira denominada la Belleza, Tiferet, cuyo nombre es יהוה, Jehovah. Sus atributos son la especulación iluminadora, el árbol de la vida, el placer, la línea media, la línea verde que rodea al mundo, la ley escrita, el gran sacerdote, la salida del Sol, las especies púrpuras, las setenta y dos naciones de la tierra, su sello es la verdad de Adán; el misterio que se halla en la tercera letra del Tetragramaton, el hombre supremo y Adán del Cielo, árbol plantado en medio del Paraíso. A través de Tiferet Dios fluye en el orden de las virtudes, y, por lo tanto, a través de la Inteligencia Rafael en la esfera del Sol. Es la causa de toda la armonía y belleza que contemplamos en el mundo. |
|
CLASSIS IV. CABALA HEBRÆRVM - CAPVT VIII. Athanasii Kircheri. OEDIPI ÆGYPTIACI. Tomus Secundus. GYMNASIVM. ROMÆ - Anno M DC LIII. |
En la Kabala, la Jerusalén Celeste suele asociarse con Tiferet, entendido como centro, núcleo y corazón del Ser.
Caso C - Deducción del punto medio del Árbol Sagrado:
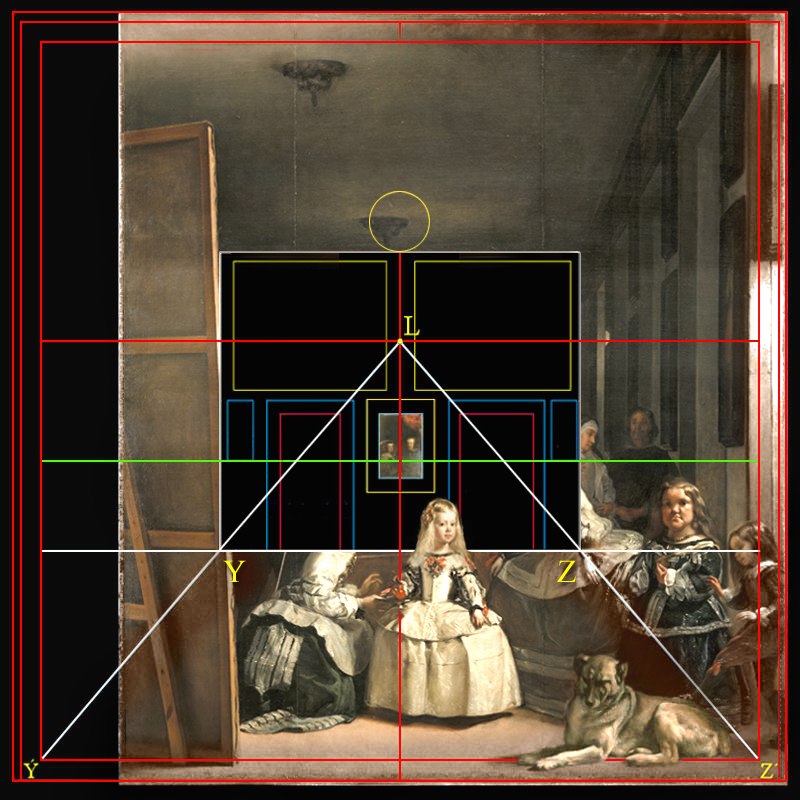 |
En este tercer caso la cuadrícula: Línea de acotación, de 144 x 144 unidades, regula el tamaño de la anchura exacta de la pared del fondo, y, además, acomoda las dos esquinas inferiores del suelo, Y y Z, de esta misma pared. |
En estas imágenes que proponemos de proporción cuadrada se analiza, al fin y al cabo, los típicos puntos invisibles y calientes de una composición pictórica [11], lo que se denomina el dibujo interno, es decir; el disegno, el soporte de la base del color; fruto de la imaginación, del entendimiento y de las calidades del artista [12].
Y científicamente, coordenadas concretas que expresan un método, y, por supuesto, total precisión.
Caso D - Deducción del punto medio del Árbol Sagrado:
 |
|
|
Velázquez sitúa en el Espejo a la Sefira nº 9, Yesod, El Fundamento, en la coordenada: [0, -9], cuya posición geométrica es centro equidistante del suelo de la Habitación del Príncipe y del punto medio del Árbol Sagrado.
El Espejo se halla dispuesto, pues, en el centro de la pared del fondo como protagonista necesario, y sublime símbolo, del significativo instante, y compleja trama, que presenta Las Meninas.
 |
||
|
Yesod IX
Shadai El Chai - El Dios Viviente Todopoderoso |
||
 |
 |
|
|
Hod VIII
Elohim Tzabaoth - Dioses de los Ejércitos |
Nectzah VII
Jehovah Tzabaoth - Dios de los Ejércitos |
|
 |
||
|
Malkhut X
Adonai Ha Aretz - Señor de la Tierra |
|
|
Poca duda nos ha quedado después de haber restituido, geométrica y matemáticamente, la inadvertida utilidad del punto L:
Caso A
Caso B
Caso C
Caso D
Y es el centro, ahora sí, del Árbol Sagrado de la Vida de la Kabala.
|
|
El dibujo
vectorial, y siempre ayudados
de una cuadrícula geométrica superpuesta al lienzo de Las Meninas,
ha sido la clave del desarrollo empírico.
Partimos bajo los siguientes supuestos:
La reivindicación del linaje real en el séptimo aniversario de la boda del rey Felipe IV.
La proclamación de la Infanta Margarita de Austria a la causa dinástica.
La solicitud del pintor Diego Velázquez para hacerse noble.
Y ciertamente, este preámbulo es la salvaguardia de un ardid tendido con el beneplácito del rey, pero en la total soledad del pintor, que le obligó al encubrimiento para que la idea más íntima no se revelara [13]:
NEC A QUO NEC AD QUEM - NI DE QUIÉN NI PARA QUIÉN.
El razonamiento de las verdades geométricas ha puesto al descubierto el fiel argumento original de esta pintura barroca.
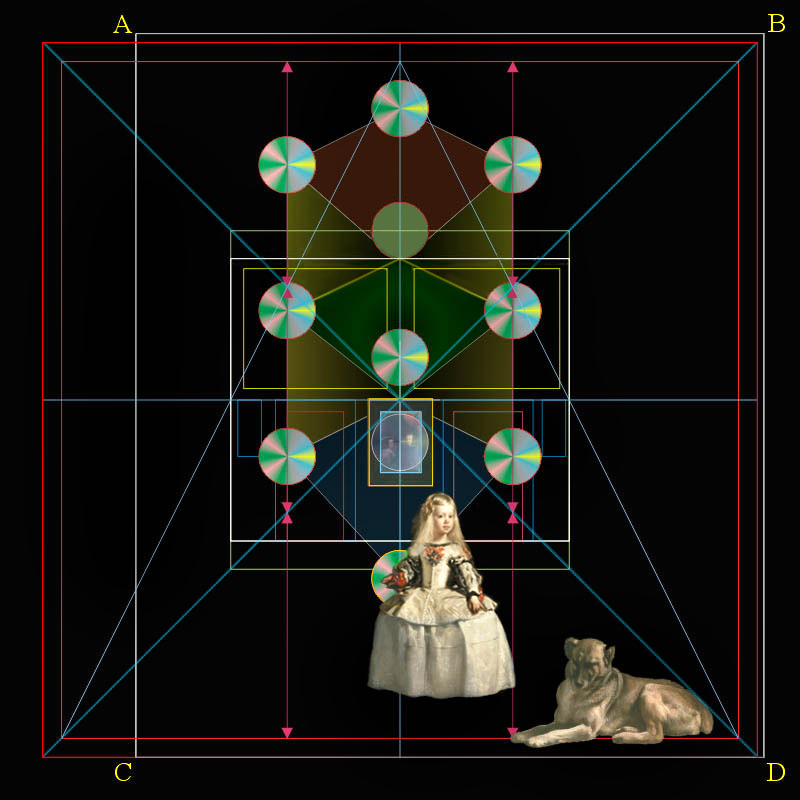 |
El Árbol Sagrado de la Vida de Las Meninas
En la coordenada [-24, -12] encontramos, puntualmente, el centro de la cruceta del Hábito de la Cruz de Santiago, en el centro del espejo se localiza la coordenada [0, -9] y en la jarrita de arcilla roja de Tonalá, Méjico, ubicamos la coordenada [0, -38].
Nos referimos a los centros de las esferas:
|
|
עשר ספירות בלימה במספר עשר אצבעות חמש כנגד חמש וברית יחיד מכוון באמצע במילת הלשון ובמילת המעור׃ |
Diez Sefirot en el vacío: Ordenadas como el número de los diez dedos. Cinco frente a cinco, y la Alianza del Único orientada hacia el centro, como la circuncisión de la lengua y la circuncisión del miembro. |
|
|
Básicamente, estas diez esferas, o diez Sefirot, representan en el espacio aéreo de Las Meninas diez atributos divinos distintos y pertinentes, más una denominada Dahat, el Conocimiento, que la mostramos tangente a la arista superior de la pared del fondo sugerida en verde claro.
La interpretación cabalística de la Geometría de Las Meninas ha confirmado, pues, nuevas respuestas y verdaderas revelaciones que exigen, en este momento, máxima sinceridad; y que, sin menoscabo alguno, son producto del estudio y práctica de antiguas ciencias conocidas como esotéricas.
Como reseñamos:
Hemos acomodado en un mapa de coordenadas el Árbol Sagrado de la Vida sobre la superficie de este lienzo.
Y aunque el derecho divino del rey emana de la voluntad de Dios, y de ninguna otra autoridad temporal, lo cual justifica la legitimidad de un monarca, porque, elegido por Dios, sólo es responsable ante Él, es indudable que el honor del rey Felipe IV, al mismo tiempo, dependía arteramente del pintor, ya que esta pequeña flaqueza convertía a un secreto en un enorme peligro, en una corte que obligaba al soberano a ser totalmente dependiente de sus ministros, de la caza, del montaje fastuoso, de sus amantes y de sus pecados.
 |
1538 Ticiano Francisco I
Musée du Louvre
Paris |
 |
1656 Velázquez Felipe IV
National Gallery
Londres |
Felipe IV depositó plena confianza en Diego Velázquez, y decidiría, el 16 de Febrero de 1652, nombrarle el nuevo Aposentador Mayor, jurando su cargo el 8 de Marzo.
Cuatro años más tarde, en 1656, apremiaba en Palacio la designación de la heredera, y, como Aposentador Mayor, a Velázquez le asistía el derecho a estar presente, autorretratado, en Las Meninas, en la que puso en juego una gran carga simbólica [14].
|
Quando ſe jura Principe, pone la ſilla donde ſe ha de ſentar; y en los Reynos donde es jurado le toca por derecho. He viſto en la que fue jurado el Rey don Iayme de Aragon, y en ella fue jurado el Rey Filipe III. Otra preeminencia es tener llaue de toda la Casa Real, ſin que aya puerta que eſtè cerrada para el. Quando en Palacio ay maſcaras, comedias, torneos y ſaraos, conſulta con su Mageſtad el orden que ſe ha de guardar en todo. |
En el despertar del Renacimiento europeo, en 1519, el monje franciscano Jean Thenaud le dedica al rey de Francia, Francisco I [15], 1494 - 1547, un tratado completo sobre la Kabala:
La saincte et tres chrestienne Cabale, metrifiée...
|
|
La saincte et tres chrestienne Cabale, metrifiée...
O cler, auguste et tres serenissime Roi des Françoys, monarque illustrissime (..).
En la clarté de gloire lumineuse Sans separer et pour jamais eureuse (..).
Quaternariae rei compendium ad disciplinas omnes scientiasve, maxime autem methaphysicas et divinas mathematicasve assequendas idoneum.
Hac itur ad occlusa sapientiae recondita et ad regnum Caroli Valaesii regis, populique Franci nutu atque benevolentia: Ismaeli, atque Esau armigero, Abrahamici stirpis natu majoribus, operam in Christo Dei (quamprimum dabuntur otia) pollicetur. MDLXVII.
JEHAN THENAUD 1519.
Bibliothèque Nationale de France. |
Thenaud en este libro apela a la tradición de los padres de la iglesia, la cual se había renovado por el neoplatonismo del siglo XV gracias a Marcilo Ficino, y a las nuevas elucubraciones sobre las jerarquías angélicas, de la Trinidad y del microcosmo; aunque Thenaud, a la par, también criticaba a la Kabala supersticiosa de los magos y la de los hebreos.
El rey francés, y no quedando muy satisfecho de este exquisito trabajo, opinó; que era mejor ser ignorante, que preguntar o buscar lo que no se puede saber sin la complicidad de la mentira.
Años más tarde, en 1536, Jean Thenaud preparó un nuevo manuscrito titulado: Introducción a la Kabala, también dedicado al rey Francisco I, sobre el mundo angélico y el espiritual.
¿Se podría juzgar la curiosidad del rey francés malsana?
El perfil del rey Felipe IV
Si hablásemos sólo de
pinceladas mágicas en
Las Meninas la cuestión sería bien diferente; Velázquez, entonces, no
habría empujado o sometido a nadie a su trabajada finalidad hebraica, es decir; sería un
tema personal e intransferible, pero esto lo dudamos.
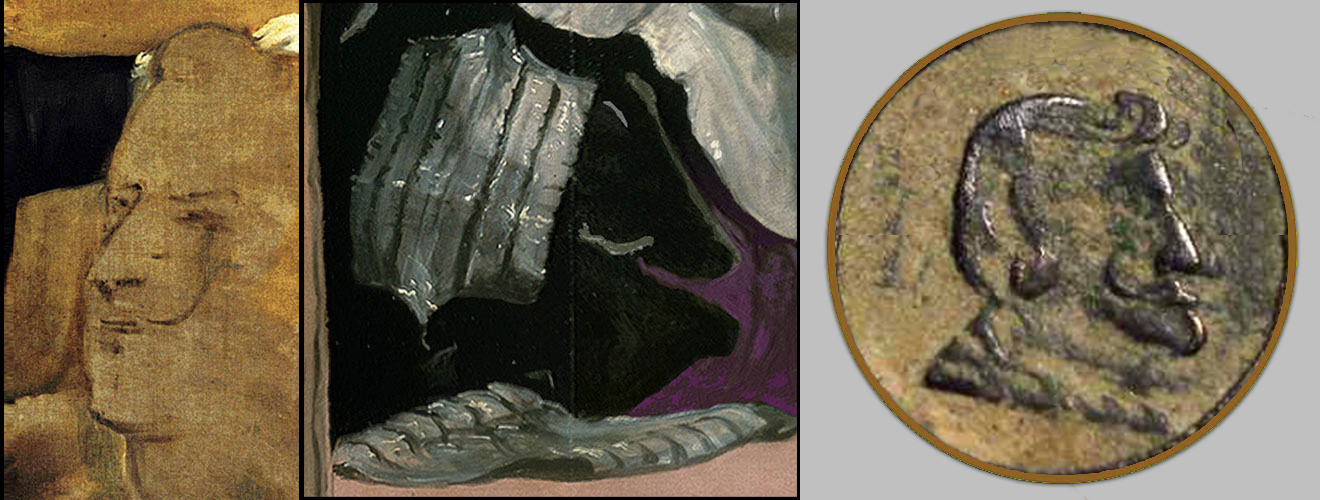
No nos echemos atrás, y observemos un emblema hexagonal manifiestamente furtivo en las luces resaltadas de los pliegues de la falda de la menina María Agustina Sarmiento.
 |
|
|
Miremos bien en la falda de la menina María Agustina Sarmiento, y descubramos, no sólo una simple enseña hexagonal diseñada y bordada por unas afanosas y cómplices costureras, sino la invitación a este barbecho de Kabala Práctica.
El resultado visual trata del perfil camuflado del rey Felipe IV contiguo al lado derecho del sello de Salomón [16].
|
Un entrecejo muy alto, de cabellos largos plateados, estrecha frente, casi cerviz, pesada y larga nariz y, por otra parte, un exuberante labio inferior gigante abre paso a la gangosa boca de este busto, sobre el que se dibuja a las claras las líneas esculturales de su bigotudo perfil... |
Detrás de esta decoración hexagonal se hallan los pies del pintor, o podemos ya decir; que esta alegoría salomónica se encuentra rendida ante Velázquez como altar propiciatorio.
Se necesitan, pues, ojos educados para sopesar la intención que subyace tras el barniz de este óleo, e, igualmente, de habilidad para lograr reconocer la identidad de estos signos, que, en su día, sirvieron para expresar ideas y frases concretas, que, como buen ejemplo, a los pies del pintor, en la zona que más depende de su futura nobleza, observamos, pues, en el bajo de la falda de la menina una licencia pictórica, que, al descifrarla, nos remonta al recuerdo de un episodio bíblico en Egipto.
|
|
|
Parashat BO - Éxodo 10:1 - 13:16
Significados:
|
|
Parte inferior de la falda de la menina Sarmiento |
Y en lo concerniente a los versículos de la Torah, Éxodo 10:1 - 13:16, éste sería su resumen:
|
Jehovah manda la octava y novena plaga, la de las langostas y la de la oscuridad, pero, aún así, el Faraón rehúsa a dejar libre a los israelitas. Es entonces cuando Jehovah revela a Moisés que la décima plaga matará a todos los primogénitos, y, para salvaguardar a los primogénitos israelitas, Jehovah ordena degollar un cordero y pintar con su sangre las puertas de sus casas.
Finalmente, el Faraón les permitirá partir de Egipto después de la muerte de su propio heredero. |
Hemos resaltado, en el borde inferior de la falda de la menina Agustina Sarmiento, dos letras hebreas que hacen mención directa a la decimoquinta Parashat BO, no obstante, en el calendario hebreo su lectura estaba fijada para el Sábado día 6 del undécimo mes Shevat del año 5417, día que corresponde al 20 de Enero de 1657, cuya marca se sitúa en la misma posición de la cruceta de la Cruz de Santiago, en el horizonte zodiacal de esta composición artística, en el 0º Acuario.
|
|
|
20 de Enero del año 1657 |
Y continuando con la falda de la menina, recordaríamos que cualquier caricatura consiste, y lo sabemos por los muchos ejemplos que se conocen, en el realce de los defectos físicos, y, a veces, morales, de un retratado, que Velázquez plasmó en los errores que la caprichosa genética se encargó de transmitir de padres a hijos en la familia de los Austrias.
El antecedente de este retrato licencioso en la falda de la menina María Agustina Sarmiento, lo hallamos, pues, en el retrato de Martínez Montañés de Diego Velázquez
 |
Este cuadro, de la colección del Museo del Prado, número de Catálogo 1194, muestra la efigie del rey Felipe IV, bosquejado con suave pincel, en la preparación del busto en barro del monarca para una escultura en bronce realizada por Pietro Tacca. |
 |
|
|
La similitud que encontramos se descubre cuando apreciamos:
La nariz, el bigote y el mentón, o mandíbula prognática; una característica fisonómica común en los herederos de tan grandioso rey y Emperador: Carlos I de España y V de Alemania.
Así que, no vemos halagos de parte de Velázquez hacia su rey, sino un uso de la imagen del monarca con fines difíciles de imaginar, aunque intentamos filtrar la idea de un retrato caricatura del monarca revestido con cuestiones relacionadas a la transmisión, a su hija la Infanta Margarita, del Reino de Jerusalén, es decir; el rey comparece en esta mancha oscura de la falda de la menina como personificación del rey Salomón.
|
Busto del Rey Salomón
En la inscripción: Salomón Rey de la Tierra de Israel
Kosher Shekel - Holanda siglo XVII - Moneda de plata - 28 mm. de diámetro |
|
Si los Austrias tenían el deber moral de preservar, defender y propagar la fe como brazo armado de la Iglesia Católica, entonces, y al mismo tiempo, se hace imposible entender el silencio histórico de su secreta religiosidad.
Aunque a decir verdad, la religiosidad a cubierto se trasforma en estigma e inquebrantable deber [18]:
|
Babilonia representaba para los escritores criptojudíos el símbolo de la tiranía, que, a su vez, simbolizaba a la misma España. Y, además, con el nombre del Sabio de Babel era conocido el Gran Inquisidor General. |
La obsesión de los Austrias por legitimar la herencia del rey Salomón podemos constatarla de distintos modos:
La corona imperial del Sacro Santo Imperio Romano Germánico llevaba la leyenda Rex Salomon.
La Orden del Toisón de Oro anhelaba recuperar Jerusalén en una nueva gran Cruzada.
El entronque salomónico, como máxima aspiración de los Austrias, culminaría en el Officium Salomonis que se iluminó en 1520 en Flandes para el Emperador Carlos V.
La planta del Monasterio de Escorial está basada en las descripciones del Templo de Salomón de diversos autores antiguos.
Las estatuas de David y Salomón flanquean la entrada de la Basílica del Palacio del Escorial.
En el Monasterio del Escorial la imagen de Salomón se sitúa en el centro de la Biblioteca, en el fresco con la Reina de Saba.
La imagen del rey Salomón, como ya hemos observado en Las Meninas, quedó reservada para el propio rey Felipe IV; al igual que la representación de Salomón, en el centro de la Biblioteca del Escorial en una pintura al fresco del pintor Pellegrino Tibaldi al lado de la Reina de Saba, corresponde, pues, al alter ego de su abuelo Felipe II.
|
|
OMNIA IN NUMERO, PONDERE ET MESURA
TODO TIENE NÚMERO, PESO Y MEDIDA |
|
|
|
Esta alusión al rey Prudente, Felipe II, en este fresco donde se representa a Salomón resolviendo los acertijos que la reina de Saba le propone, se está plasmando, pues, la legendaria sabiduría que caracterizó a este rey bíblico.
Ante viento y marea la Kabala permaneció agazapada en sus rescoldos, sin embargo, ha espoleado la curiosidad de los más poderosos debido a la creencia de quien poseyera su conocimiento controlaría las fuerzas animadas del universo.
Y en conclusión; una vez optimizado el uso de Kabala Práctica en Las Meninas, entonces, ahora deberíamos aceptar, de buen grado, la muy resuelta y desatrancada invitación velazqueña.
Convencimiento
Al igual que todo
artista católico, Velázquez bosqueja la imagen divina
hebrea como un único Dios revelado, y, con
acentuado antropomorfismo, pintó unidos a los dos ancianos de la Kabala:
El Macroprosopus & el Microprosopus.
Y ahora daremos una gráfica respuesta:
 |
El Macroprosopus velazqueño
La luz de Dios como textura del pañuelo que sujeta en la mano izquierda la reina Mariana de Austria.
אריך אנפין
Arich Anpin - El Largo Rostro - El Macroprosopus - El Anciano de los Días
Veamos lo que el texto cabalístico Idra Zuta, texto que se considera una de las enseñanzas más profundas del Zohar, revela al respecto:
En el libro la Sagrada Asamblea Menor, Idra Suta, ſeu Synodus minor, nos encontramos la descripción de este enigmático rostro representado en el pañuelo blanco del retrato de la reina Mariana de Austria.
|
SECTIO IV.
De oculis Senioris Sanctiſſimi.
§.113. Oculi capitis Senioris Sanctiſſimi duo ſunt in uno, æquales, qui ſempe proſpiciunt & non obdormiſcunt.
Acerca de los ojos del Anciano de los días
§.113. Los ojos de la cabeza del Santísimo Anciano son dos en uno, iguales, que siempre miran hacia afuera & no duermen. |
En El Zohar leemos:
|
|
|
Idra Zuta - Pequeña asamblea
La apertura de los ojos
Verso 28
Los ojos en la cabeza de Atika Kadisha, es decir, Arich Anpin, cuyo dos ojos se consideran uno. Siempre están vigilantes, nunca dormidos, como está escrito: “He aquí, que el guarda a Israel, no se adormecerá ni dormirá” (Tehilim 121:4), es decir, el santo Israel, que es Zeir Anpin, por tanto, no tiene cejas ni párpados sobre los ojos. |
En otro de los libros que componen El Zohar leemos:
|
38. Nasso: 8.
Verso 52
§.141. El virtuoso y el más digno verán en el futuro este ojo de Arich Anpin con espíritu de sabiduría. Ésto es lo que está escrito: Para aquellos que vean el ojo ante el ojo (Isaías 52:8). ¿Cuándo ésto sucederá? : Cuando Hashem vuelva a Zion (Ibid.). Y además está escrito: Que Tu Hashem eres contemplado ojo ante el ojo (Números 14:14).
§.142. Si no fuera por el ojo supremo de Arich Anpin, que está siempre atento y baña más abajo al ojo de Zeir Anpin, el universo no podría existir incluso por un momento. |
DE MESSIA. Horae Hebraicae et Talmudicae. Dresdae et Lipsiae. M DCCC XLII
|
Qvoniam oculo ad oculum videbunt. Sohar Geneſ. fol. 112, 4. R. Joſe dixit: Qvoniam Deus Iſraëli bonus eſt, Iſraëli in mundo hoc & futuro portionem habebit, ut videat gloriam Dei oculo ad oculum, q.d. Quoniam oculo. Idem Exod. fol.52. col.206. Futuro tempore conſtituit Deus S.B. ſe revelare filiis ſuis, ut omnem gloriam ſuam videant oculo ad oculum, q. d. Qvoniam oculo ad oculum videbunt, qvando reſlituet Dominus Zionem. Et alibi Jeſa. XL, 5. Et videbit omnis caro ſimul. Midraſch Tehillim ad Pſalm. XIII, 1. fol. 10, 2. Dixit Deus S.B. ad Iſraëlitas: In hoc mundo faciem meam a vobis abſcondi; ſed in ſeculo futuro oculo ad oculum videbunt.
Vide Locum Generalem XVI, 1. XIX, 3. XXVII, 3. L,XX, 6. 6. XCVI, 4. CVI. |
|
Porque verán el ojo ante el ojo. Zohar Geneſ. fol. 112, 4. R. José dijo: Porque el Dios de Israel es bueno, Israel tendrá porción en este mundo y en el futuro, para que pueda ver la gloria de Dios ojo ante ojo, q.d. Porque con el ojo. En el mismo Éxodo. fol.52 columna 206. En el futuro, Dios estableció S.B. revelarse a sus hijos, para que vean toda su gloria ojo ante ojo, q. d. Porque se verán ojo ante ojo cuando el Señor restaure a Sion. Y Jesús en otra parte. XL, 5. Y toda carne se verá junta. Midrasch Tehillim ad Pſalm. XIII, 1. fol. 10, 2. Dios dijo S.B. a los israelitas: En este mundo escondí de vosotros mi rostro; pero en la era venidera verán el ojo ante ojo.
Ver Lugar General XVI, 1. XIX, 3. XXVII, 3. L,XX, 6. 6. XCVI, 4. CVI. |
זעיר אנפין
Zeir Anpin -
Pequeño Rostro - El Microprosopus - Pequeño Semblante

EL
MICROPROSOPUS VELAZQUEÑO
Y, cierto es, que si Velázquez, autor de tan dispuesta celada, está usando a la Kabala como medio de expresión artística, su mensaje consiste en promover un alegato inseparable al contexto ritualista de esta materia.
El espacio aéreo de Las Meninas
Y aunque estas nuevas
observaciones
podrían desalentar al más entusiasta del arte de la pintura, son, sin embargo,
los fundamentos esenciales que explican el mensaje interno de Las Meninas, y, responde, de una vez, a la
demandada explicación de la singularidad artística del pintor Diego Velázquez.
El tono de esta investigación está salvaguardada por dos circunstancias interdependientes;
de un análisis que justifica una Geometría Matemática coherente,
y de una nueva condición simbólica que prueba la trascendencia de esta pintura.
 |
|
El punto L tiene por coordenadas: [0, 12], ahora bien, analicemos en la imagen también el vector ÝZ´, correspondiente al lado inferior del cuadrado que llamamos; Línea de acotación, que se halla, a su vez, implicado como base del triángulo, ÝLZ´, donde dos de sus medianas; ÝZ y Z´Y, además, desvelan las dos esquinas del suelo de la pared del fondo. |
Una vez afianzada la Geometría descubriremos en el espacio aéreo de esta pintura la ubicación puntual de los Sefirot; aunque, según cuenta la tradición, sería un acto temerario reanimar estas esferas sin la suficiente preparación, ya que la mente podría quedar inmersa en la riqueza de sus atributos, por lo que, en este caso, nos ceñiremos a localizarlas en un espacio ya provisto de límites geométricos.
La pared del fondo, tal y como explicamos en el desarrollo de este estudio, queda dividida en doce partes iguales.
 |
|
|
Queremos dejar constancia de que este plano, mapa o cuadrícula, tiene una lectura universal dentro del conocimiento científico, difícil o fácil de explicar, pero que puede ser estudiado con aprendizaje un tanto especializado, pues, terciamos con la mismísima Kabala.
La siguiente imagen especifica el enclave de los puntos calientes y cabalísticos que tratamos.
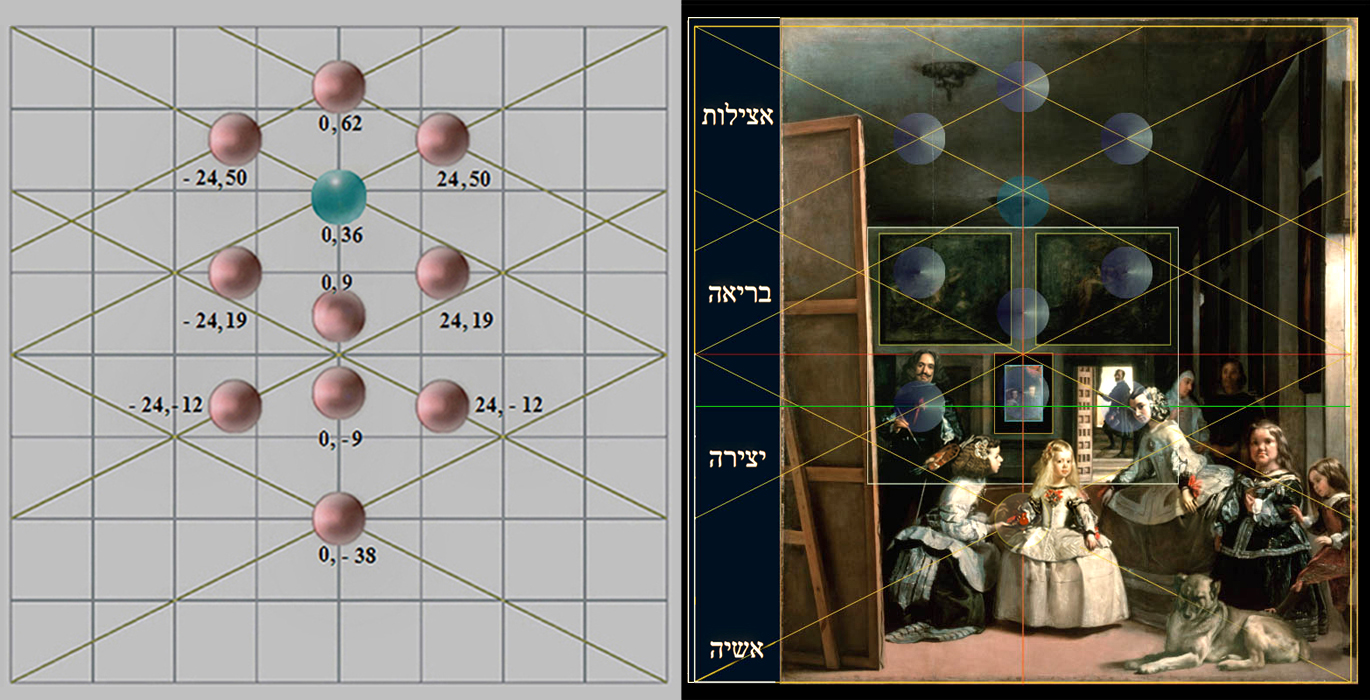 |
|
|
La raíz cuadrada de 5 aparece en la fórmula del número áureo, y es geométricamente la hipotenusa de un triángulo rectángulo cuyos catetos miden 1 y 2 respectivamente.
Todos los datos que aportamos son factibles de ser representados, indistintamente, en un tablero de dibujo profesional o en un programa informático editor de gráficos vectoriales; puesto que hablamos de herramientas que secundan la ubicación idónea de los 10 Sefirot + Dahat en el espacio aéreo de Las Meninas.
notas a pie de página
1 - Libro I - Theorema. 33. - Propoſitio. 47.
En los triangulos rectangulos el quadrado que es hecho de el lado que eſta opueſto al angulo recto es ygual a los dos quadrados que ſon hechos de los lados que contienen el angulo recto.
|
|
Sea el triangulo rectangulo .ABC. que tenga recto el angulo BAC. digo que el quadrado que es hecho del lado .EC. es ygual a los quadrados que ſe hazen de .BA. y de .AC. Deſcribaſe, por la .46. de la .BC. el quadrado .BDCE, y por la miſma, de la BA. y de la, AC. los quadrados .ABZI. ACKT. y por el punto A. tireſe .AL. parallela con la .BD. CE, por la propoſicion .31, y por la .I. peticion tireſe AD. CZ. y porque los angulos. BAC. BAI. ſon rectos. Luego tiradas dos lineas rectas .AC. AI. deſde vna linea recta .AB. y deſde vn punto en ella .A. no hacia vnas miſmas partes hacen de vna y otra parte angulos yguales a dos rectos por la .14. propoſition, luego en derecho eſta la .AC. de la .AI y por eſto tambien BA eſta en derecho de .AT y porque el angulo .DBC. es ygual al angulo .ZBA. porque cada vno dellos es recto; pongaſe comun el angulo ABC. Luego todo DBA es ygual a todo el angulo ZBC. y porque las dos .AB. BD. ſon yguales a las dos BZ. BC. la vna a la otra, y el angulo .DBA es ygual al angulo .ZBC. luego la baſis .AD, por la .4. propoſicion, es ygual a la baſis .ZC. y el triangulo .ABD. al triangulo .ZBC. es tambien igual. Y el parallelogramo .BL, por la 41, es doblo del triangulo .ABD porque tiene vna miſma baſis que es .BD. y esta en vnas miſmas parallelas, es a ſaber .DB. AL. y tambien el quadrado .IB. por la miſma, es doblo del triangulo .ZBC. porque tiene la miſma baſis que es .BZ. y eſta en vnas miſmas parallelas, es a ſaber .ZB. IC. y las coſas que ſon doblo de coſas yguales, por la .6. comun ſentencia, entre ſi ſon yguales. Luego el parallelogramo .BL. es ygual al quadrado .IB Semejantemente ſi por .I. peticion, ſe tiran .AE BK. ſe demoſtrara el parallelogramo CL. ſer ygual al quadrado .TC. Luego todo el quadrado .BDEC, es ygual a los dos quadrados .IB, TC. Y el quadrado .BDEC. es hecho de la .BC. y los quadrados IB. CT. ſon hechos de la .BA. AC. Luego el quadrado que de el lado .BC. ſe hizo es ygual a los quadrados que ſon hechos de los lados .BA. AC. luego en los triangulos rectangulos el quadrado que es hecho del lado que eſta oppueſto al angulo recto y lo que mas ſe ſigue como en el theorema, que ſe hauia de demoſtrar. |
| Demostración |
LOS SEIS LIBROS PRIMEROS DE LA GEOMETRIA DE EVCLIDES - Traduzidos en lengua Eſpañola por Rodrigo Çamorano Aſtrologo y Mathematico, y Cathedratico de Coſmografia por ſu Mageſtad en la caſa de la Contratacion de Seuilla. Dirigidos al illuſtre ſeñor Luciano de Negron, Canonigo de la ſancta ygleſia de Seuilla. Con licencia del Conſejo Real. En Seuilla en caſa de Alonſo de la Barrera. 1576.
2 - Catálogo de Pedro Ruiz Pérez: De la Pintura y las Letras. La Biblioteca de Velázquez, editado por: E. P. G. Conserjería de Cultura. Junta de Andalucía. 1999.
Lista de libros relacionados con la Aritmética, Geometría y Arquitectura:
|
· 415. - Antonio Buscon, De Architectura italiano. · 417. - De fortificacion cat. Yomo Castrioro. · 419. - Vitrubio de Arquitectura. · 420. - Matemática de Aguilon. · 421. - Galasso Matematica en dos tomos. · 422. - Architectura de Vicencio Escamacio beneciano. · 423. - Alberto Durero, Simetria italiano. · 424. - Cataneo de Architectura italiano. · 425. - Jeometria de Bitelono. · 427. - Architectura de Leon Alberti. · 428. - Sebastian Serlio, Architectura. · 433. - Vitrubio, Architectura. · 440. - Geometría práctica. · 448. - Elementos de Euclides. · 450. - Matemática de Pedro Cataneo. · 461. - Perspectivas de Euclides. |
· 462. - Perspectivas de Daniel Barvaro. · 463. - Arismetica de Moya. · 464. - Vitruvio de Architectura. · 466. - Serguio, De Architectura. · 467. - Numeros y medidas. · 468. - Nicolao Tartalia en italiano. · 469. - Vitruvio, Architectura en italiano. · 470. - Juan Antonio Buscon, Architectura. · 478. - André Palladio de Architectura. · 480. - Algebra de Pedro Nuñez. · 490. - Especularia, en italiano. · 491. - Marco Aurelio Alemán. Arismetica. · 493. - Céspedes de Geometría. · 497. - División de superficies, italiano. · 498. - Summa Astrológica. · 503. - Perspectiva de Euclides. |
· 507. - Aritmetica de Joseph Unicornio, italiano. · 508. - Baptista Alberto, italiano. · 511. - Euclides filósofo. · 516. - Antonio Fineo, Aritmética. · 519. - Materia de Architectura. · 532. - Practica de perspectiva, italiano. · 533. - Jacomo Barrocio de Architectura. · 536. - Serlio de Architectura. · 538. - Pedro Cataneo de Architectura. · 545. - Sciencia Matematicas de Nejarense. · 551. - Mobimiento de los planetas. · 553. - Antonio Labaco, Architectura. · 554. - Alberto Durero, Geometría. · 556. - Architectura de Vitrubio, italiano. · 558. - Leonardo de Vinci, de la pintura. · 561. - Pedro Antonio Darca de Architectura. |
3 - Página 202 - Libro IX - I DIECI LIBRI DELL´ARCHITETTURA DI M. VITRVVIO. Tradutti et commentati da Monsignor Barbaro eletto patriarca d'Aquileggia. Venecia. MDLVI.
Hauendo queſto Pithagora ritrouato, non dubitando di non eſſer ſtato in quella inuentone dalle Muſe ammonito riferendole grandisſime gratie ſi dice, che le ſacrificaſſe uittime, & quella ragione come in molte coſe, & in molte miſure è utile, coſi ne gli edificij per fare le ſcale, accioche ſiano i gradi di proportionata miſura, e molto ſpedita, perche ſe l’altezza del Palcho da i capi della trauatura al liuello, & piano da baſſo ſerà in tre parti diuiſa, la ſceſa delle ſcale ſerà cinque parti di quelle con giuſta larghezza de i fuſti, e, tronchi; perche quanto grandi ſeranno le tre parti dalla ſomma trauatura al liuello di ſotto, quattro di quelle ſi hanno à tirare in fuori, & ſcoſtarſi dal dritto, perche coſi moderate ſeranno le impoſte de, i, gradi, & delle ſcale, & ancho di tal coſa la forma ſerà diſſegnata.
Y escribe el español Iuan Perez de Moya en la página 95 - Tratado de Geometria Practica y Speculatiua - Alcala - M. D. LXX. III.
|
|
De otro modo podras prouar ſi es vna eſquadra perfecta. Abre el compas en vna quantidad conueniente, y contando en el vn lado, ò linea de la eſquadra (començando del punto a.) tres tamaños ſemejantes à la diſtancia de la abertura del compas, como en la linea a. c. de la ſiguiente figura denotan las letras d. e. f.
Luego toma en el otro lado, ò linea a. b. quatro tamaños ſemejantes à eſtos como denota g. h. i. k. Saca agora vna linea recta deſde el punto f. haſta el punto k. y ſi eſta linea tuuiere cinco tamaños ſemejantes a los tres que tomaſte en el lado a. c. ò a los quatro del lado a. b. la tal eſquadra ſera verdadera, y ſi ay menos, o mas tamaños de cinco eſtara falſa, como ſe prueua por la penultima del primero de Euclides. Porque ſi el angulo a. es recto, el quadrado de la linea a. f. y a. k. ha de ſer ygual al quadrado de la linea f. k. que es lado opueſto al dicho angulo recto, pues ſi el lado a. f. tiene tres tamaños, y en el a. k. tiene quatro, la ſumma de los quadrados deſtos numeros 3. y 4. es 25. Luego el otro lado f. k. es neceſſario que tenga cinco tamaños, para que ſu quadrado haga veynte y cinco, que es lo que haze la ſumma de los quadrados de los otros lados que comprehenden el angulo recto. Ha ſe dicho eſto aquí porque como con eſte inſtrumento ſe ha de moſtrar medir diſtancias, es bien ſaberle hazer. |
4 - Se atribuyen a Tales de Mileto varios descubrimientos matemáticos registrados en los Elementos de Euclides:
La definición: I. 17.
Y las proposiciones: I. 5 - I. 15 - I. 26 - III. 31.
Libro III - Theorema. 27. - Propoſition. 31.
En el circulo, el angulo que eſta en el medio circulo es recto, y el que eſta en el ſegmento mayor, es menor que recto, y el que en el menor ſegmento, es mayor que recto. Y de mas de eſto el angulo del mayor ſegmento es mayor que recto; y el angulo del menor ſegmento es menor que recto.
LOS SEIS LIBROS PRIMEROS DE LA GEOMETRIA DE EVCLIDES - Rodrigo Çamorano. Seuilla. 1576.
5 - Página 454 - Petri Gassendi. Animadversiones in decimum librum Diogenis Laertii, qui est De Vita, Moribus, Placitiſque. EPICVRI. Lugduni. M. DC. XLIX.
Relata iam antè duo ſunt: Vnum, quo Zeno contendebat non poſſe vunquam inchoari motum; quia cùm ex ſpatio quolibet, percurri priùs debeat dimidium vicinius, quàm remotius; & talis dimidij ſit rursús dimidium vicinius, quod percurrendum prius ſit; ac eiuſce dimidij pari ratione aliud, illiúſque aliud atque ita in infnitum, abſque eo, quòd detur vnquam primum momentum, quo accipi prius poſſit, & in quo non dimidij dimidium ſuperſit; ideò nunquam pateat ingreſſus in ſpatium; neque adeò motus inchoari poſſit. Alterum, quo deducebat fore, vt mobile celerrimum nunquam aſſequi ſegniſſimum poſſet, vt Achilles Homero πόδας ὠκύς pedibus celer, teſtudinem. Quoniam cùm nullum ſit momentum, in quo teſtudo non conficiat partem ſpatij tantulam, quam, aut ipſi æqualem vt Achilles ſuperet, momento vno opus ſit; neque in Achillis motu ſint plura momenta, quàm in motu teſtudinis, ideò nunquam Achilles tantum versùs teſtudinem progrediatur, quim teſtudo, tantundem Achillem præcedat; ſicque iſte illam nunquam aſſequatur.
6 - Reductio ad absurdum, reducido a lo absurdo.
Método lógico en donde se prueba de que la hipótesis está equivocada demostrando que sus consecuencias son absurdas, imposibles o ilógicas.
7 - Libro I - Definición 4
Linea recta es la que ygualmente eſta entre ſus puntos.
LOS SEIS LIBROS PRIMEROS DE LA GEOMETRIA DE EVCLIDES - Rodrigo Çamorano. Seuilla. 1576.
8 - Alegoría de una las siete artes liberales; la Geometría, basada en el libro de Marciano Capella: De nuptius Philologiae et Mercurii.
|
|
Alegoría de la Geometría del Siglo XIV
La alegoría femenina sujeta en su mano izquierda una escuadra, y con la derecha manipula un compás sobre un tablero de dibujo redondo. Enfrente de ella, un grupo de diez monjes observan, con animada atención, el estudio de la práctica geométrica. |
La traducción de Gerardo de Cremona, del libro de los Elementos de Euclides, comienza con una letra P mayúscula en el códice Miscelánea escolástica atribuido al Maestro Melician.
9 - En el Sefer Yetzirah, cuyo texto es el tratado más antiguo del mundo contemplativo hebreo, se describe el proceso cosmogónico mediante la combinación de las 22 letras hebreas; letras que equivalen a los ladrillos de los que se sirve el Arquitecto Divino para la construcción del mundo.
En el Tomo I / Página 151: OEDIPVS AEGYPTIACVS - ATHANASII KIRCHERI - ROMAE. MDCLII. Libro dedicado al emperador Fernando III, el padre de Mariana de Austria, es decir; el suegro y cuñado del rey Felipe IV, Athanasius Kircher lo menciona con el nombre R. Abraham in Iethſira.
Hinc in arbore Sephiroth apud Cabaliſtas גמדות ſeu tres proprietates Deo affinguntur, quibus Deum omnia feciſſe memorant, ſuntque . בִּינָה . חָכְמָה . כֶּתֶר Corona, Sapientia, Intelligentia; quas R. Abraham in Iethſira appellat מספר ספר סופר id eſt, numerantem, numerum, & numeratum; quae tria exacte reſpondent tribus ſupra a Iamblicho citatis nominibus, Amun, Phtha, Emepht.
Los diez Sefirot, como principios sagrados, representan cualidades divinas por las que Dios revela algo de su esencia que determina el Árbol Sagrado de la Vida.
La palabra Sefira, singular de Sefirot, סְפִירוֹת, deriva de varios vocablos; de Sefer texto o narración, de Sefar o número y de Safira o piedra preciosa transparente.
En el primer capítulo del Sefer Yetzirah, al explicar la creación del Universo, se hace un juego de palabras con la raíz de este término:
Y Él creó Su Universo con tres libros, ספרים, Sefarim,
בספר - Sefer, con texto o narración,
וספר - Sefar, con número
y, וספור - Sipur, con comunicación.
Mientras que Athanasius Kircher, en el año 1652, propone la siguiente traducción:
מספר ספר סופר id eſt, numerantem, numerum, & numeratum.
10 - La construcción de un espacio sagrado se inicia a partir de un centro; en el dibujo a pluma que mostramos de Federico Zuccaro, 1542 - 1609, en el centro geométrico se localiza una gran hostia consagrada guarnecida por unas cortinas, y, justo delante, se distingue el sarcófago del Mesías, en este caso de Jesucristo, y que, a su vez, se haya flanqueado por las alegorías de Moisés, a la derecha, y la de Elías, a la izquierda.
En la Kabala cristiana la Sefira nº 6, Tiferet, se asocia con Jesucristo; tal y como se dispone en el ejemplo del dibujo de Federico Zuccaro.
|
|
|
Federico Zuccaro
Metropolitan Museum of Art - New York |
En 1527, en la iglesia del Santo Sepulcro de Milán, se exhibió por primera vez el santo Sacramento para ser adorado con el fin de propiciar la intervención divina en tiempos de calamidades y guerras durante un periodo de cuarenta horas.
La celebración de la Cuaresma fue institucionalizada en 1592 por el Papa Clemente VIII en el documento Graves et diuturnae, Instructio Clementina, y en el siglo XVII, Urbano VIII, en la encíclica Aeternus rerum Conditor de 6 de agosto de 1623, ordenó la celebración de la Cuaresma en todas las iglesias del mundo católico.
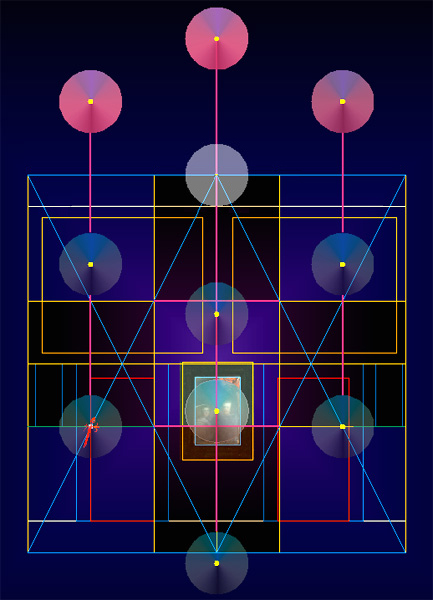
11 - Regla de los Tres Tercios:
La denominada regla de los Tres Tercios divide la escena de la pared del fondo en tres partes iguales; tanto horizontal como verticalmente, y establece los centros de interés de Las Meninas.
|
|
 |
|
|
Como señalamos:
La cruceta de la Cruz de Santiago, en el corazón de Diego Velázquez, es un punto fuerte y llamativo de máximo interés compositivo.
La Ley del Horizonte
El Horizonte de Las Meninas está situado a la altura de 1/3 respecto a la arista baja artificial de la pared del fondo de acorde con la Ley del Horizonte, que dice; que hay que situar el Horizonte a 1/3 del suelo si se trabaja con espacios amplios y profundos para privilegiar a la profundidad.
12 - Desde la Academia de San Lucas de Roma, su fundador Federico Zuccaro, y en su obra: La idea de pintores escultores y arquitectos, publicada en Turín, 1607, se define el dibujo interno con estas palabras:
Per questo nome di disegno interno io non intendo solamente il concetto interno formato nella mente del pittore, ma anco quel concetto che forma qual si voglia intelletto.
Por el nombre de dibujo interno yo no entiendo solamente el concepto interno formado en la mente del pintor, sino además aquel concepto que se forma por deseo del intelecto.
De acuerdo a esta teoría el diseño interno viene a ser una prebenda divina, pues es en el espíritu del artista donde preexiste, como idea formada en su mente, para poder conocer la realidad última de las cosas.
De lo que se deduce; que la calidad del diseño interno estará en proporción con la información ya alojada dentro de su mente, y que la modelará, más tarde, gracias a su intelecto.
Federico Zuccaro trabajó en el Monasterio del Escorial para el rey Felipe II.
13 - Diego Saavedra Fajardo, Empresas Políticas. Edición de Milán de 1642.
 |
NEC A QUO NEC AD QUEM
Sin que se descubran los pasos de sus designios.
EMPRESA - 44
Dudoso es el curso de la culebra torciéndose a una parte y otra con tal incertidumbre, que aun su mismo cuerpo no sabe por dónde le ha de llevar la cabeza; señala el movimiento a una parte, y le hace a la contraria, sin que dejen huellas sus pasos ni se conozca la intención de su viaje. |
14 - Página 333 - Libro Tercero. De la Casa Real y sus oficios. Teatro de las Grandezas de la Villa de Madrid. Corte de los Reyes Catolicos de Eſpaña. Al muy poderoso Señor Rey Don Felipe Qvarto. Por el Maestro Gil Gonzalez Davila. 1623. Madrid.
15 - Ibid., página 310. El rey de Francia, Francisco I, era un viejo conocido en el Palacio Alcázar; el bisabuelo de Felipe IV, Carlos V, tras la batalla de Pavía el 24 de febrero de 1525, lo trajo preso a Madrid.
|
Otra torre donde eſtuuo preſo el Rey Franciſco de Francia: antes de ſubir à ella ay vna galeria, que llaman del Cierço, adornada con retratos de los Reyes de Portugal, mapas, y pinturas varias. |
16 - Estudio de las 23 intersecciones en el Hexagrama.
En esta ilustración contemplamos la posición de las 22 letras hebreas, y en el centro el planeta o elemento Tierra.
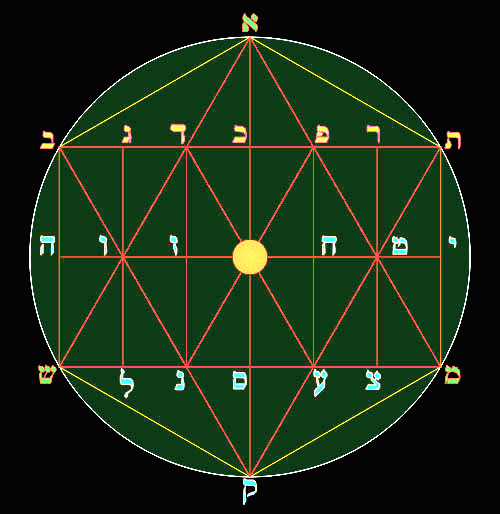 |
 |
Abordaremos los nombres más conocidos de esta forma geométrica y hexagonal:
Maguen David = Escudo de David.
Tzion = Sión.
Hexagrama o estrella de seis puntas.
Sello de Salomón.
Estrella de David.
Muchos nombres y apellidos para ensalzar una imagen genuina de la herencia mágica primitiva del patrimonio de la humanidad, y, simultáneamente, revelarnos el desarrollo de la Matemática y Geometría por parte de los griegos y sus sucesores en toda la cuenca mediterránea.
17 - Martínez Montañés fue un escultor de madera tallada y policromada. Nació en Alcalá la Real, Jaén, en 1568, y muere en Sevilla en 1649.
18 - Libro Verde de Aragón escrito en 1507 por el asesor de la Inquisición aragonesa Juan de Anchias, junto al memorial presentado al rey Felipe II por el cardenal Mendoza y Bobadilla, arzobispo de Burgos, llamado Tizón de la Nobleza de España, son dos únicos documentos que ponen de manifiesto, sin lugar a dudas, la existencia de sangre judía en el clero y en la nobleza, ya que fueron confeccionados a partir de los Archivos de la Inquisición:
Hablamos, pues, de dos libros: Uno en la sociedad aragonesa y el otro en la castellana.
El Consejo aragonés acudió al rey Felipe IV suplicando la destrucción del Libro Verde a los cien años de la redacción del manuscrito, y será el Consejo de la Inquisición quien recoja y destruya todas sus copias, como se demuestra por el Decreto existente en el tomo IV de Decretos originales, al folio 330, aunque, afortunadamente para la historia presente, fue encontrado un ejemplar, procedente del Archivo del Consejo de la Inquisición, en la Biblioteca Colombina de Sevilla.
El Decreto de Felipe IV, agradeciendo al obispo de Cuenca, Andrés Pacheco, el celo con que le había ayudado en la retirada del libelo, reza así:
|
Por el Consejo de Aragon se me ha presentado la diligencia y cuidado que habeis hecho poner en recoger el Libro que llaman Verde en aquel Reyno. Agradezcoos lo que haveis dispuesto en esto y por ser cosa de la calidad que es, y convenir que no quede ni aun rastro del dicho Libro, os encargo que hagais continuar las diligencias tan apretadamente como conviene y lo espero de vuestro celo.
Señalado de Su Majestad en Madrid, a diecisiete de Noviembre de 1623.
Al Inquisidor General. |
|
INICIO |
|
Aplicación del Pie Real |
|
El Árbol de la Vida |
|
El Escudo de Armas |
La Escalera |
La Perspectiva |
La Pared del fondo |
El Espejo |
|
|
La Herencia |
|
La Sagrada Simbología |
|
|
La Astrología |
Buena medición |
La Paleta del pintor |
Los Planos |
La Divina Proporción |
|
|
El color del Aire |
|
La Puerta |
|
|
Acotación |
La Paz de los Pirineos |
La Perspectiva de la Puerta |
La Infanta Margarita |
El Teorema de Pitágoras |
|
|
Coordenadas |
|
El Corazón |
|
|
La Espiral |
|
El Centro |
|
El Bastidor |
|
Marian de Austria |
Braccio fiorentino |
|
|