|
|
[ resolución gráfica 1920 X 1080 ] |
|
|
[ resolución gráfica 1920 X 1080 ] |
|
|
El Árbol de la Vida
Ante lo meramente estético, lo esencial en el estudio
de una obra de arte es recuperar el mensaje que se emite, y, en consecuencia,
que explique el porqué de su invención, no obstante, la genialidad de
Diego Velázquez, como se demuestra en el caso del óleo de Las
Meninas, todavía se halla en el proceso de conocerse, ya que,
es del todo cierto, que eminencias de las ciencias, letras y artes desdeñaron la
sospecha del apego del maestro español a una de las herencias más prohibida de
la península Ibérica:
La ley de Boca, también llamada La Kabala.
Dentro de este amplio estudio, mediante un cuidadoso examen se ha logrado trazar un plano detallado gracias a la rehabilitación del sistema de medidas castellano, un trabajo de reconstrucción que permite, por primera vez, adentrarse en la riqueza simbólica de esta obra de Velázquez, también conocida como La Familia de Felipe IV, y descubrir, pues, distintas capas de significados, que dan pie a una nueva lectura de esta icónica representación de la realeza española.
Este análisis profundiza, pues, en aspectos que hasta ahora habían pasado desapercibidos en la explicación de Las Meninas, y desafía, no obstante, las interpretaciones tradicionales, lo que obliga a reconsiderar, en el contexto de la España del siglo XVII, el inexplorado vínculo de esta escena pictórica con la superstición y la doble moral en la casa de los Austrias.
Como premisa, el Árbol de la Vida representa, pues, un testimonio del poder sacro, y, más allá de su etérea apreciación, advierte a todos los seguidores velazqueños a estar al tanto de la desconocida personalidad, y de una amplia gama de secretos reveladores, del genio indiscutible de la pintura española.
Y es en el modo de dar vida a lo material, y su destreza de fusionar realidad y falsas apariencias, donde se aprecia la intención de la obra de Velázquez, cuyo legado perdura en la historia del arte universal.
Operamos, pues, con un margen de seguridad de una diezmilésima de unidad en los resultados matemáticos que aportamos.
Es decir; de una cantidad equivalente a 0,0001 de unidad [1].
|
|
X = 20,666666 x 0,0001 / 1 = 0,002066 milímetros.
En conclusión; 0,002066 milímetros representaría el margen de seguridad de cualquier dato numérico que especifiquemos, aunque propiamente hablando a este margen de seguridad le correspondería esta cantidad de micras:
|
|
X = 0,002066 milímetros x 1000 micras / 1 milímetro = 2,066666 micras [2].
Teniendo en cuenta que el grosor del cabello humano mide entre 17 a 180 micras, y que un glóbulo rojo tiene de diámetro de 5 a 7 micras.
Medimos, pues, con la ayuda de una cuadrícula de trabajo que, como herramienta, revela dos cuestiones fundamentales;
el mensaje oculto de Las Meninas,
y el tamaño exacto de este lienzo.
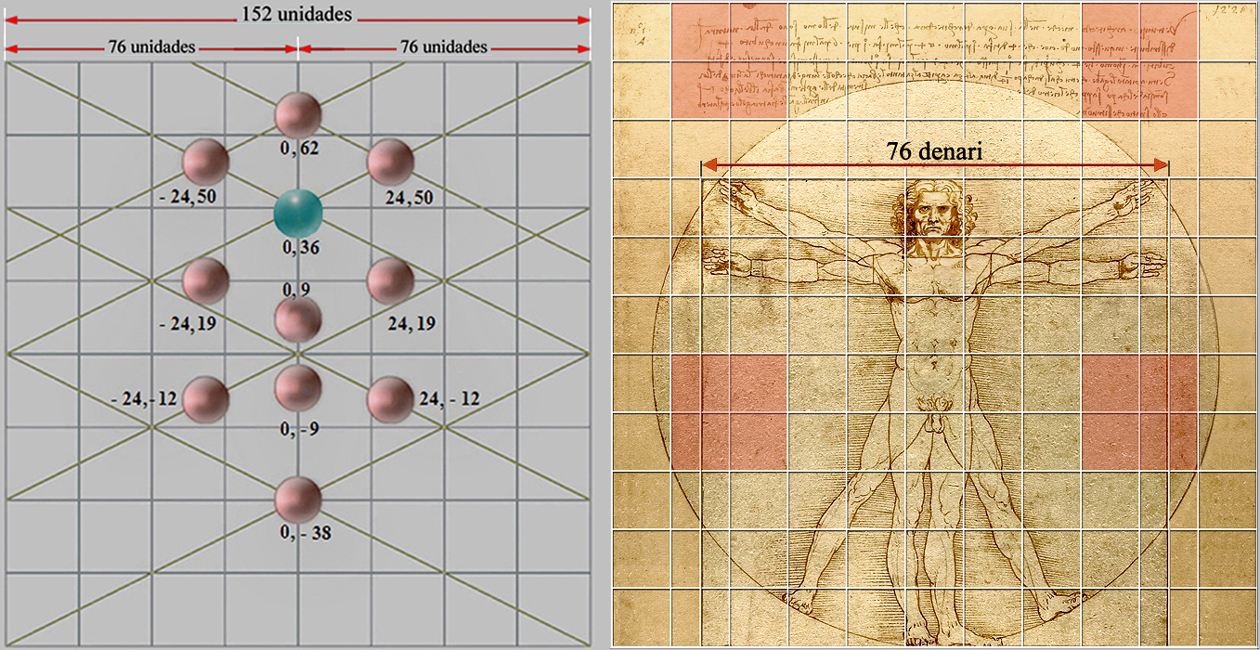
No obstante, en el lado del cuadrado que inscribe la altura y anchura del Hombre de Vitrubio se emplea el número 76, nos referimos, pues, a una cantidad contenida dos veces en el tamaño del lado de la cuadrícula de trabajo de 8 x 8 cuadrados que utilizamos para analizar el óleo de Velázquez.
Y, antes de continuar, añadiríamos que Leonardo da Vinci también utiliza una cuadrícula de de 8 x 8 cuadrados, donde cada subcuadrado mide 9,5 denari de lado, lo que multiplicado por 8 sumaría un total de 76 denari florentinos, por tanto, en el papel, la altura del dibujo del Hombre de Vitrubio mediría:
76 denari x 0,243055... cm. por denaro = 18,472222... cm.
 |
|
|
Y dada la antigüedad de Las Meninas, se entiende, pues, que cualquier dato acerca de su formato requiere el visto bueno de las reglas de Geometría, y el empleo de números enteros y racionales, y sus equivalentes en el sistema de medidas castellano, para la salvaguardia del cálculo aritmético.
| Unidad |
Pulgadas por unidad |
Milímetros por
unidad |
|
1 |
8/9 = 0,888888... |
20,666666... |
|
|
| unidad | pulgada | milímetro |
El cálculo aritmético que mostramos no es convencional, sino rigurosamente exacto.
 |
 |
|
|
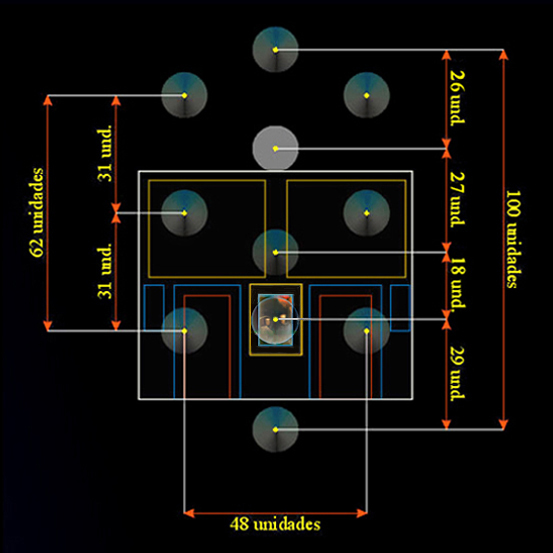
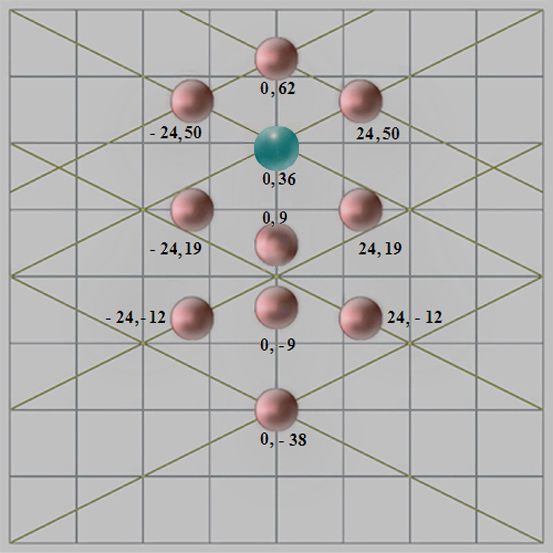
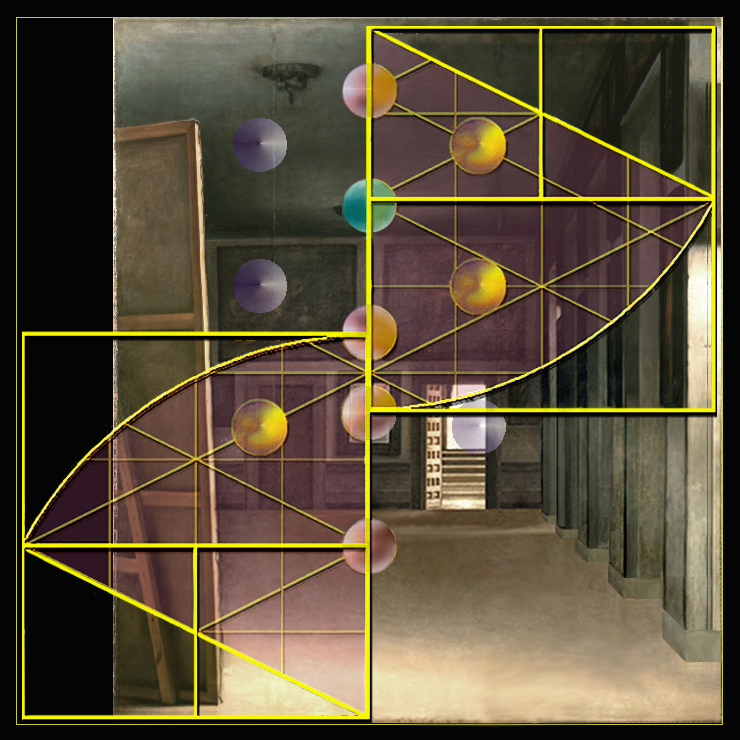
Tras inagotables indagaciones, y la ciencia apropiada, hemos asegurado en una rejilla cuadrada de 152 unidades de lado la posición de 10 + 1 esferas en coordenadas de números enteros, no obstante, estas esferas, huéspedes del aire de la Habitación del Príncipe, se disponen sobre un mapa cartesiano de, al menos, 23.104 coordenadas posibles, y atesoran la idea de que bajo el logrado naturalismo de esta obra maestra se conserva una pensada reivindicación.
Operamos, pues, en una gran cuadrícula graduada en medidas castellanas como soporte geométrico de los llamados diez Sefirot del Árbol Sagrado de la Vida, que consolida la simetría del escenario pictórico, y confirma, además, que en una antigua restauración el tamaño de esta obra maestra fue levemente alterado [3].
El Árbol de la Vida se origina en un punto de luz primordial e infinita que se expande a partir del centro de la esfera superior en los demás Sefirot.
|
|
|
|
Aunque sea el lienzo de Las Meninas el resultado del estudio de una amplia gama de efectos del claro y oscuro de la luz, y de sus tonos grises, sin embargo, tuvimos que buscar en ciertos libros prohibidos el origen de su velada inspiración; un esfuerzo que tomó sentido práctico gracias al hallazgo del Sefer Yetzirah, conocido también como el Libro de la Formación [4].
En la lectura del Sefer Yetzirah se pone de manifiesto, pues, la importancia del valor numérico de ciertas palabras en base a los números pitagóricos por excelencia; 3, 4 y 5, que son, a su vez, los números que determinan las medidas castellanas en el desarrollo geométrico de este óleo.
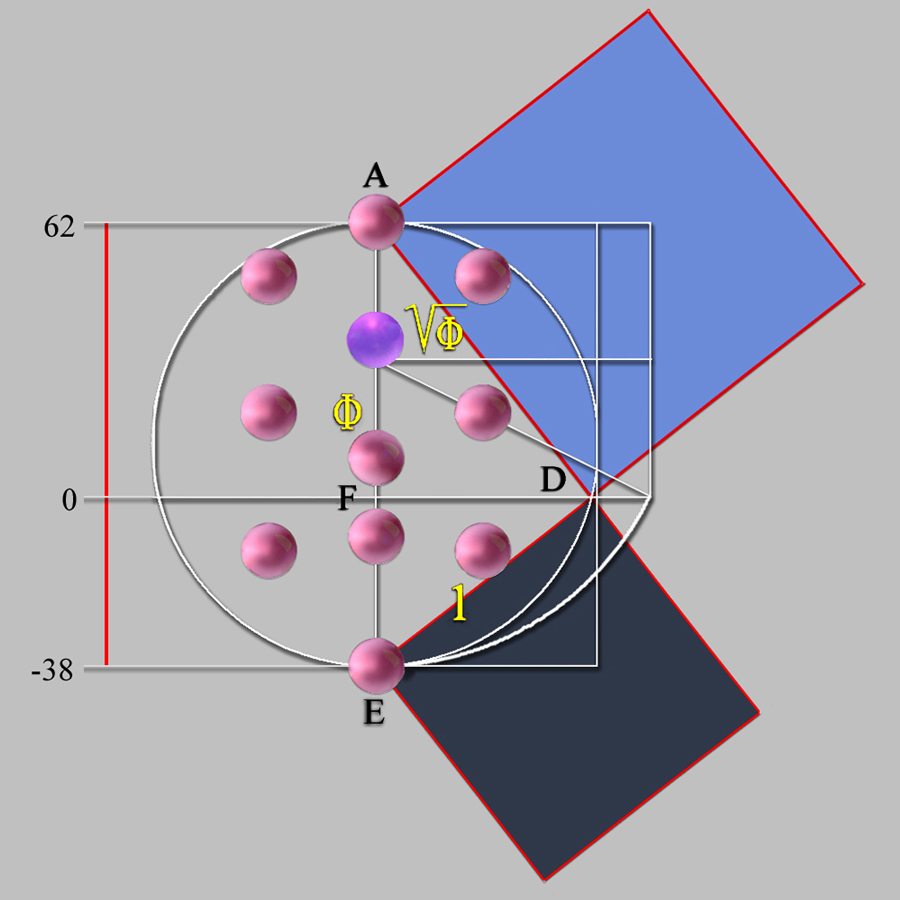
Pero, además, Velázquez, en el proceso creativo de su obra, dio un paso al frente planteando una Geometría de acorde a su época, ya que la altura del eje central del Árbol de la Vida de Las Meninas corresponde, pues, a la hipotenusa AE de la base del Triángulo Rectángulo Áureo de Kepler.
Y esta propuesta es posible porque la distancia entre el centro de la Sefira nº 1, Kether, La Corona: (0, 62) y el centro de la Sefira nº 10, Malkut, El Reino: (0, -38), mide, exactamente, 100 umidades, es decir; un múltiplo de 10 de acorde al punto (3) Latus AE 10 = 10 del análisis del Problema del triángulo áureo del año 1597 planteado por Michæl Mästlin, el maestro de Kepler.
 |
AE |
AD |
ED |
|
10 |
√61,803398... |
√125 - 5 |
|
|
10 |
7,861513... |
6,180339... |
|
|
MICHÆL MÄSTLIN |
|||
|
Φ |
√Φ |
1 |
|
|
1,618033... |
1,272019... |
1 |
|
|
100 |
78,615097... |
61,803398... |
|
|
VELÁZQUEZ |
|||
|
|
 |
|
|
 |
|
|
Si bien, en este renglón habría que remarcar, pues, dos cuestiones que justifican la elección de esta Geometría áurea:
El punto F, en el triángulo de Kepler, está localizado en la misma posición que el centro de coordenadas E, centro de la Geometría de Las Meninas,
y que las medidas de los tamaños de los tres lados del triángulo áureo que descubrimos en el aire de este lienzo no sólo tratan de cifras, sino cantidades en unidades que son equivalentes, por tanto, a las pulgadas castellanas.
 |
La trama del Sefer Yetzirah está inspirada, pues, en los tres elementos primarios; fuego, agua y luz, אש ,מים ,אור, en donde la palabra luz, אור, se transforma en el vocablo aire, אויר, agregando una letra yod, י, es decir; un aire cuyas cuatro letras permutadas revelan la mirada prístina, וירא, del espíritu creador.
|
Y vio Dios que la luz era buena; y Dios apartó a la luz de las tinieblas.
וירא אלהים את האור כי טוב ויבדל אלהים בין האור ובין החשׁך׃
Génesis 1:4 |
|
FUEGO |
AGUA |
AIRE |
LUZ |
|
אש |
מים |
אויר |
אור |
| 300 + 1 | 40 + 10 + 40 | 200 + 10 + 6 + 1 | 200 + 6 + 1 |
Y será en el Renacimiento cuando se dé a conocer este manuscrito de tradición oral gracias a los comentarios de Joseph Gikatilla, 1248-1325, que fueron transcritos por Paulus Ricius, del hebreo al latín, en su libro Portæ Lucis. Augsburgo, 1516
Del Sefer Yetzirah existen distintos comentarios e ediciones impresas:
Paulus Ricius. Portæ Lucis - Augsburgo. 1516
Ioannis Revchlin. De Arte Cabalistica - Hagenau. 1517
Guillaume Postel. Abraham Patriarchœ Liber Iezirah. París. 1552.
Sefer Yetzirah - Mantua. 1562
Johann Pistorius - Basilea. 1587
Joanne Stephano Rittangelio - Ámsterdam. 1642
Athanasius Kircher - Roma. 1652
Pero, eso sí, todos acabaron en el Índice de libros prohibidos, al menos, desde mediados del siglo XVIII.
|
Index librorum prohibitorum Sanctissimi Domini Nostri Benedicti XIV Pontificis Maximi jussu. Recognitus atque editus. Romæ. 1758. |
|
|
Lista de libros prohibidos por orden del Santísimo Señor Benedicto XIV Pontífice Máximo. Revisado y publicado. Roma. 1758. |
|
ספר יצירה |
|
|
|
Liber Formationis |
|
|
|
Libro de la Formación |
|
|
El Sefer Yetzirah es el primer tratado cabalístico que menciona las esferas del Árbol de la Vida, y aunque su estudio requiera de cierta preparación, sin embargo, ejerció una gran influencia en la mentalidad hebrea, ya que, como libro de distintas enseñanzas, incluye además el proceso de la creación divina mediante la combinación de las 22 letras hebreas; 22 letras que se comparan a los ladrillos de los que se sirvió el Arquitecto Divino para la construcción del mundo.
Las esferas que descubrimos en el espacio aéreo de Las Meninas se denominan los diez Sefirot del Árbol de la Vida, y, como principios sagrados, sus diez atributos poseen cualidades tan especiales que en ellos se descubre un asomo de la esencia divina.
|
Sefira |
Significado |
Castellano |
 |
|||
|
I |
Kether |
Corona |
רוח אלהים חיים |
El Aliento del Dios Vivo | ||
|
II |
Chokmah |
Sabiduría |
רוח מרוח |
Aliento del Aliento | ||
|
III |
Binah |
Inteligencia |
מים מרוח |
Agua del Aliento | ||
|
Dahat |
Conocimiento |
בלימה |
Nada | |||
|
IV |
Chesed |
Clemencia |
אש ממים |
Fuego del Agua | ||
|
V |
Geburah |
Fortaleza |
רום |
Arriba | ||
|
VI |
Tiferet |
Belleza |
ותחת |
Abajo | ||
|
VII |
Netzach |
Victoria |
ודרום |
Sur | ||
|
VIII |
Hod |
Honor |
צפון |
Norte | ||
|
IX |
Yesod |
Fundamento |
מזרח |
Este | ||
|
X |
Malkhut |
Reino |
ומערב |
Oeste | ||
|
|
Al final del primer capítulo del Sefer Yetzirah se enumeran los orígenes del universo que se atribuyen a los diez Sefirot, y, conjuntamente, se explica cómo se propaga el Aliento del Dios Vivo, el cual se identifica con el Espíritu Santo, y establece en el mundo; el espíritu, la voz y la palabra, más el centro de las seis direcciones del espacio.
La tradición oral hebrea se valió de la boca y del oído para conservar fuera de la vista a la Kabala, y esta vez, sin menoscabo alguno, ha sido el ojo testigo de Su fehaciente presencia en las pinceladas de esta pintura.
Haciendo justicia, pues, consideraremos la aplicación de la Kabala en la Geometría del escenario de Las Meninas, lo que supone abrir un diálogo con la Sabiduría de las diez esferas del Árbol Sagrado de la Vida trazadas en el espacio pictórico de esta obra maestra.
|
|
|
|
No obstante, este enfoque sugiere que la estructura geométrica de este lienzo no sólo refleja el alto conocimiento del pintor Diego Velázquez en las matemáticas de la perspectiva, sino también una profunda comprensión de la enseñanza cabalística, la cual se halla integrada como recurso iconográfico.
|
|
|
|
Aparentemente, pues, una explicación distante a las habituales de esta obra maestra, sin embargo, este era su legado.
Y este es el punto de inflexión:
Entre la Kabala Práctica entendida como Magia, y la Magia que realiza cosas sorprendentes; en ambos casos se usa una fórmula según el ritual acostumbrado, aunque la Magia, a diferencia de la religión, que postula la humildad y pide por medio de plegarias, se ve a sí misma como arte o ciencia.
|
Estos son los Diez Sefirot de la nada: El aliento de Dios vivo, aliento del aliento, agua del aliento, fuego del agua. Arriba, abajo, sur, norte, este, oeste.
אלו עשר ספירות בלימה רוח אלהים חיים רוח מרוח מים מרוח אש ממים רום ותחת ודרום צפון מזרח ומערב
Sefer Yetzirah 1:14 |
|
|
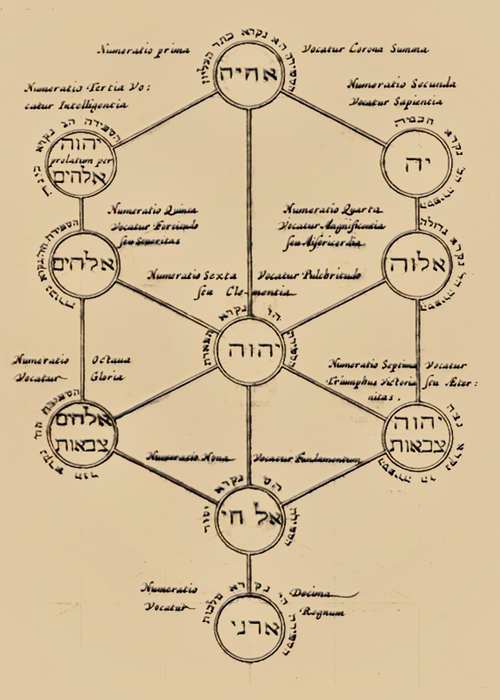
La tradición afirma que la emanación de los diez Sefirot se manifiesta en el mundo físico a través de las diez esferas del Árbol Sagrado de la Vida, y, si bien, hablamos de un legado de la milenaria andadura de la Kabala que el óleo de Las Meninas salvaguardó, también confirmamos que el reencuentro fortuito con su modelo original se produjo, sin lugar a la duda, en un grabado de un libro editado en 1642 en Ámsterdam.
El Sefer Yetzirah comentado en hebreo por Yosef ben Shalom Ashkenazi, y traducido al latín por Joanne Stephano Rittangelio.
 |
 |
|
|
Cada letra, idea, palabra o imagen de este texto fue analizada, en profundidad, por el pintor español Diego Velázquez.
El libro de Joanne Stephano Rittangelio, en pleno siglo XVII, no sólo constituye el detonante cabalístico de Las Meninas, sino que se le podría considerar el motivo de la resuelta decisión velazqueña de plasmar la sublimación del Arte de la Magia Operativa con el beneplácito de la Kabala judía.
|
|
|
|
|
|
La raíz cuadrada de 5, cuyo resultado es 2,236 con una exactitud de casi el 100%, aparece en la fórmula del número áureo, y corresponde al tamaño de la hipotenusa de un triángulo rectángulo cuyos catetos miden 1 y 2 respectivamente.
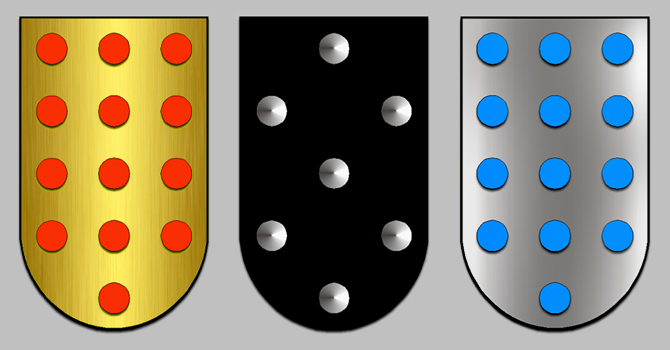
En definitiva, una estructura legendaria que es el santo y seña de Las Meninas, y que, básicamente, nos remite a la misma idea que se conserva en el despliegue geométrico de las trece roelas azules en el escudo de Armas del apellido Velázquez.
 |
Los Velazquez traen por Armas treze Roeles azules en campo de plata, y por orla ocho Aſpas de oro en campo roxo. |
|
Gonzalo Argote de Molina
Sevilla - 1588 |
El origen heráldico de los Roeles según Gonzalo Argote de Molina [5]:
|
De ſu antiguedad eſcrive Barbe Ragnault; tienen ſu principio de el Rey Artur de Inglaterra, que inſtituyó los Cavalleros de la Tabla Redonda, y les dio orden de Cavalleria, Armas y Deviſas. De los quales fueron muy famoſos Genaſio el Fuerte, Mador de la Puerta, y Perſides el Gentil. Al primero dio por Armas treze Roeles roxos en campo de oro. Al ſegundo ſiete Roeles de plata en campo negro. Al vltimo los Roeles azules en campo de plata, como oy los vſan los de Caſtro. |
El escudo de Armas de Velázquez es, por tanto, una divisa incrustada en otra idea dotada de un gran valor simbólico que nunca dejó de acompañar a su propietario.
 |
|
Genaſio el Fuerte |
Mador de la Puerta | Perſides el Gentil |
|
Este que ves entre moriscas lides Con seis azules roeles señalado, Antiguas armas del Gentil Persides, En tiempo del Rey Artus celebrado; |
| Página 109 - EL
BERNARDO, POEMA HEROYCO Bernardo de Balbuena. 1808. Madrid. |
Don Bernardo de Balbuena, Obispo de la isla de San Juan de Puerto Rico, en su libro titulado: Bernardo del Carpio, que fue impreso en Madrid en el año mil seiscientos veinticuatro, no se olvidaba de mencionar a Gentil Persides, el ancestro del pintor sevillano.
Para establecer la verdadera idiosincrasia de Diego Velázquez habría que sopesar, pues, que no sólo encontramos en su comportamiento artístico ideas morales muy distintas a sus contemporáneos, a lo que se sumaría, por su condición privilegiada de pintor del rey, el constante estímulo de un entorno sin rivales en el proceso de su redención personal.
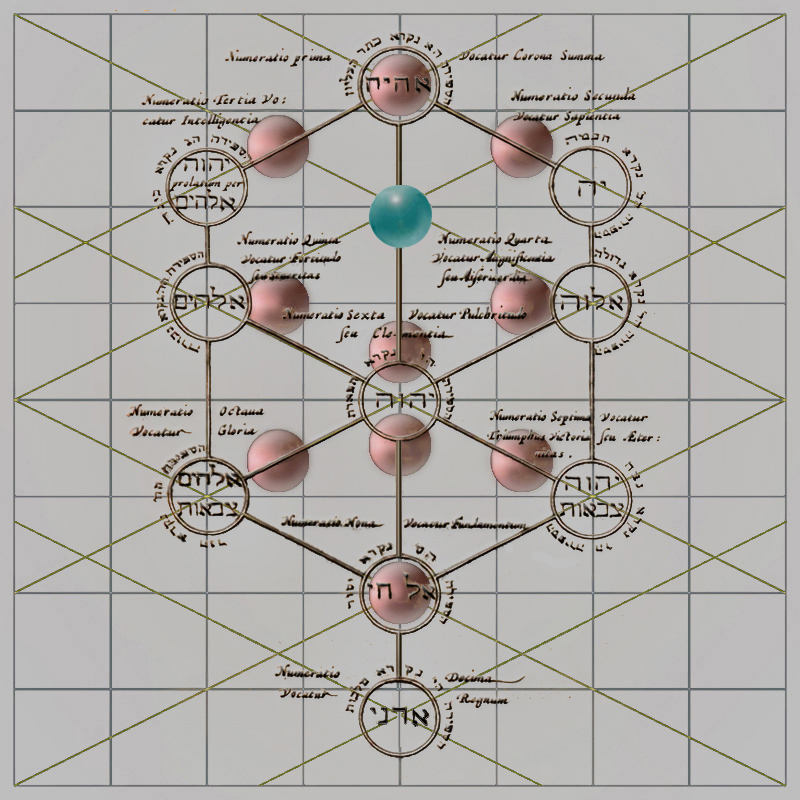
Y haciendo justicia, la siguiente ilustración confirma, pues, las características de la estructura del Árbol de la Vida del óleo de Las Meninas:
La escala: 986,7975 veces a 3,
la exactitud geométrica,
la fiabilidad del sistema de medidas en unidades
y la simbología.
 |
Numeración |
Hebreo |
Velázquez |
Rittangelio |
|
I |
Kether |
0, 62 |
0, 62 | |
|
II |
Chokmah |
24, 50 |
38, 43 | |
|
III |
Binah |
- 24, 50 |
- 38, 43 | |
|
Dahat |
0, 36 |
|||
|
IV |
Chesed |
24, 19 |
38, 19 | |
|
V |
Geburah |
- 24, 19 |
- 38, 19 | |
|
VI |
Tipheret |
0, 9 |
0, 0 | |
|
VII |
Netzach |
24, - 12 |
38, - 19 | |
|
VIII |
Hod |
- 24, - 12 |
- 38, - 19 | |
|
IX |
Yesod |
0, - 9 |
0, - 38 | |
|
X |
Malkut |
0, - 38 |
0, - 62 |
|
El Árbol de Joanne
Stephano Rittangelio. Ámsterdam. 1642 El Árbol de Diego Velázquez. Madrid. 1656 |
Hagamos, pues, la comparación de tamaños entre estos dos esquemas del Árbol de la Vida:
| Autor | centímetros | centímetros cuadrados | proporción | ||||
| Velázquez |
314,1333... |
x |
314,1333... |
= | 98679,75 | 986,7975 veces a 3 | |
| Rittangelio | 20 | x | 15 | = | 300 | ||
Y es seguro que la Geometría de este pequeño grabado holandés de 20 x 15 centímetros, que Velázquez adaptó a escala en su obra maestra, genere nuevas respuestas, ya que, ilustrando a Las Meninas con esta novedosa característica, estaríamos descifrando un asunto muy comprometido cuya envergadura supera a la sorpresa que provoca.
El pintor plantea todo un gran desafío de acuerdo con la lectura interior de esta pintura:
La aplicación de la Geometría áurea
y la enseñanza trascendente de Las Meninas.
Hablamos, pues, de una cualidad esencial de la Geometría, y de su relación con las diez esferas cabalísticas del Árbol Sagrado que coronan la sublime experiencia sensorial de este lienzo:
Un vínculo presente en Las Meninas expresado desde puntos muy concretos.
|
|
|
|
Elementos de la Geometría
La limpieza de Las Meninas en el año 1984 documentó aspectos técnicos que han dado pie a nuevas observaciones [6]; y cierto es que Velázquez, aún pintando con verismo, dejó abierta la posibilidad de sopesar más de una explicación de las distintas fases del proceso de su óleo.
Trabajamos, pues, con la copia de la placa fotográfica de 12 x 18 centímetros que se tomó durante la restauración de Las Meninas en 1984, es decir; se trata de una imagen de gran calidad de 28,9 megas en formato TIF descomprimido de 2917 por 3455 píxeles [7].
En cuanto a esta instantanea, detectamos, pues, que el chasis de la placa fotográfica, de la cámara técnica de gran formato utilizada para la ocasión, no estaba exactamente en paralelo respecto al plano horizontal del lienzo de Las Meninas; por lo que esta fotografía, ya digitalizada, la giramos - 0,3 grados en el programa Adobe Photoshop 7.0 para corregir la vertical y horizontal de la composición.
Si bien, y debido a que el bastidor de Las Meninas estaba apoyado directamente en una pared durante la toma fotográfica, y, por lo tanto, su eje vertical se hallaba inclinado, constatamos, pues, la falta de 1,18 pulgadas en la altura de la imagen, es decir; 1,3275 unidades, que representan 0,027435 metros en la imagen escaneada, aunque, afortunadamente, gracias al programa vectorial Corel Draw se subsanó este error en la foto de trabajo.
Sin duda, ha sido la Geometría que desarrollamos la que ha detectado esta inexactitud en la copia fotográfica digitalizada del 0,86... % para la altura y del 0 % para la anchura.
 |
|
|
Todo resultado numérico que aportamos se fundamenta en reglas de Geometría para no exponernos a errores, por lo que hemos empleado, en un mar de conjeturas, un modelo matemático exacto que todo el mundo debería conocer.
Tipos de cuadrículas sobre la superficie de Las Meninas:
 |
|
Estas cuatro cuadrículas de trabajo sobre la superficie de Las Meninas están sometidas al mismo sistema de medidas y coordenadas, ya que mantenemos como centro de este plano el punto E situado en la parte superior del espejo.
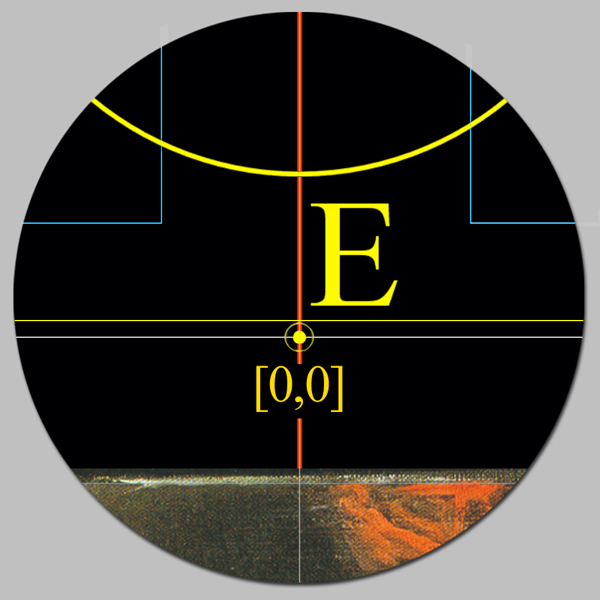 |
[0, 0]
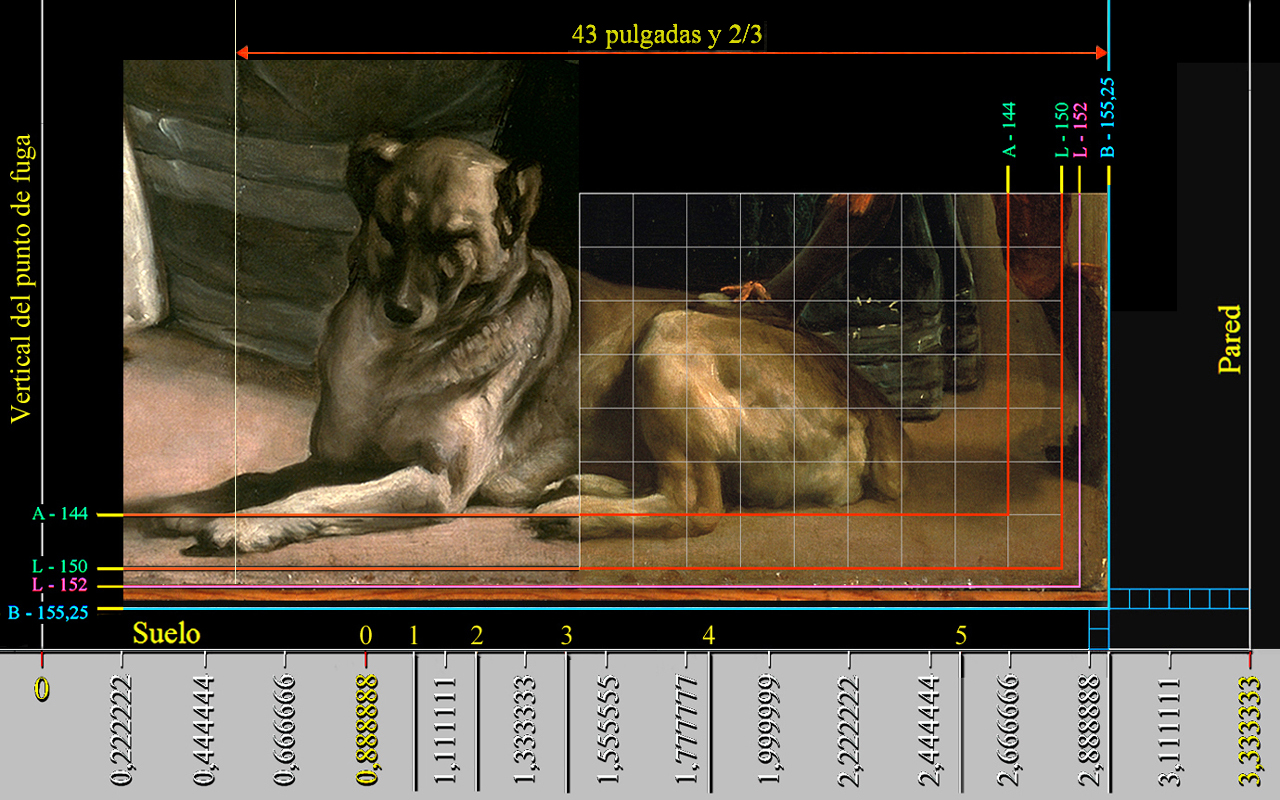
| Modelo | Cuadrículas | Lado en unidades | Lado en pulgadas | Abscisa X | Ordenada Y |
| A - 144 | Línea de acotación | 144 | 128 | 0 | 0 |
| L - 150 | Límite de la rejilla de 150 unidades | 150 | 133 y 1/3 | 0 | 0 |
| L - 152 | Límite de la rejilla de 152 unidades | 152 | 135 y 1/9 | 0 | 0 |
| B - 155,25 | Borde del orillo del lino original | 155,25 | 138 | 0 | 0,375 |
|
Y señalaríamos que el perímetro del lienzo de Las Meninas queda acotado, por su lateral derecho y superior, por la cuadrícula de trabajo de 155,25 unidades equivalente a 138 pulgadas.
La Geometría de Las Meninas fue proyectada, pues, a partir de un cuadrado de 3,141333... metros de lado, y equivalente a 152 unidades, cuyo centro quedó instalado en la parte superior del marco del espejo con los reyes de España reflejados en su interior [8].
 |
 |
|
|
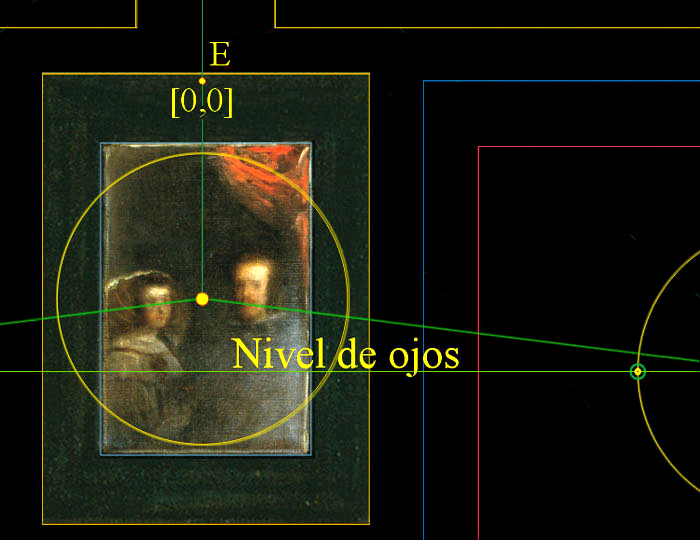
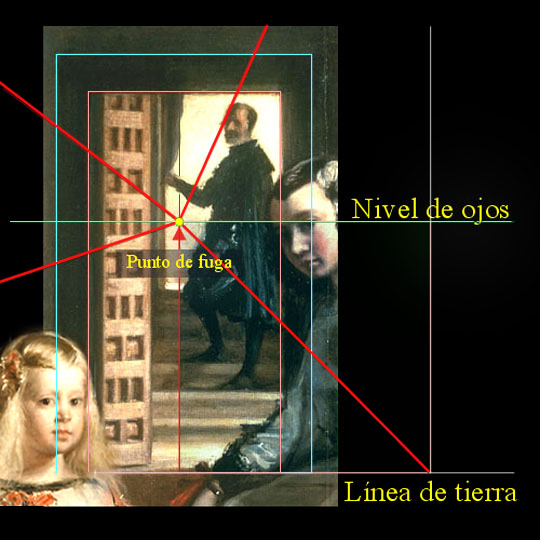
Conjuntamente, y de acuerdo a la realidad, el pintor Diego Velázquez propuso un complejo análisis de efectos de luz, estableciendo un punto de fuga áureo, como origen matemático de la perspectiva, en la refulgente y última pared de la pieza arquitectónica, justo detrás de la puerta semiabierta de veintidós cuarterones, para que, de forma inmediata, indujera al espectador a un entorno de tres dimensiones [9].
Esta profundidad está ayudada, pues, por los cuarterones oblicuos de la puerta semiabierta, y esta sensación es notable en la pared sur derecha, en donde se alinean las ventanas y los cuadros colgados, lo que crea un ambiente natural.
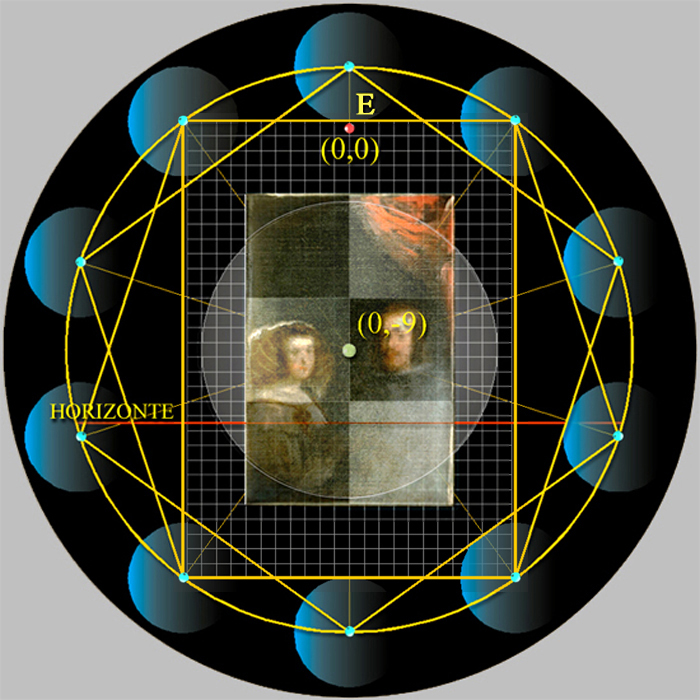
Y como culminación del esfuerzo del pintor no hay duda acerca de la perspectiva aérea, pero, sorprendentemente, venía acompañada de diez principios sagrados desplegados etéreamente en el aire de Las Meninas, y, de igual número, que los diez círculos que circundan el marco gótico del espejo de la tabla de Van Eyck [10].
Diez círculos que relatan la Pasión y Resurrección de Cristo, y transforman al espejo en un objeto sagrado.
 |
 |
|
National Gallery de Londres - firmado en el año 1434 por Jan Van Eyck |
Resaltamos, pues, la preocupación de Jan Van Eyck, como también la tuvo Diego Velázquez 222 años después, la de centrar su óleo, de estilo primitivo y flamenco, gracias a un espejo.
En ambas pinturas se asocia al espejo con la alegoría del matrimonio, como ejemplo y modelo, y con lo que se capta en sus superficies más allá del ámbito pictórico, es decir, el mundo real.
 |
|
|
Estas similitudes son preludio de una ingeniosa idea en la que ambos espejos quedaron vinculados por medio de la figura de un decágono, formado por dos pentágonos superpuestos, en cuyos diez vértices se situaron los centros de los diez círculos que los rodean:
Tanto en el caso de la disposición de los diez círculos en el marco del espejo de Van Eyck,
como los que determinaron el formato del ancho y alto del marco de madera del Espejo de Las Meninas.
De modo, que a partir de este esquema, Velázquez disponía en el Espejo a la Sefira nº 9, Yesod, el Fundamento, donde el rey Felipe IV y la reina Mariana de Austria refrendan, desde entonces, una Alianza divina.
 |
 |
|
|
|
No obstante, Velázquez, en la variedad de su estilo naturalista, en el Espejo pinta la presencia de los monarcas con doble apariencia; la reflejada en el Espejo y su ausencia ante el lienzo.
La unificación
Damos a conocer, pues, un patrón geométrico de unidades longitudinales que pone de acuerdo al Pie Real Castellano del rey Felipe II con el Metro francés de Napoleón Bonaparte.
|
Magnitud |
Año |
Divisiones |
Milímetros |
Pulgadas | Unidades |
|
Pie Real Castellano del rey Felipe II |
1568 |
12/12 |
279 |
12 | 13,5 |
|
Metro francés de Napoleón Bonaparte |
1800 |
1000/1000 |
1000 |
43 y 1/93 | 48 y 12/31 |
Desde el año 1872, es decir; de acuerdo con las medidas del catálogo del Museo del Prado, las medidas del lienzo de Diego Velázquez se han mantenido seguras durante 150 años, por lo que el desglose de la anchura y altura de Las Meninas sería el siguiente:
| Tamaño | Museo del Prado | Sistema métrico | Sistema castellano | Unidades |
| Anchura | 2,76 metros | 2,759 metros | 118 pulgadas y 6/9 | 133,5 |
| Altura | 3,18 metros | 3,182666 metros | 136 pulgadas y 8/9 | 154 |
DEMOSTRACIÓN
En base a la altura de 3,182666 ... metros del lienzo de Las Meninas, relacionaremos, pues, su tamaño con el lado de una cuadrícula cuadrada de 150 unidades de lado, y, como se puede observar en la siguiente tabla, se constata que al lado del Límite de la rejilla de 150 unidades le correspondería;
3 varas, 2 pies, 1 pulgada y 4 líneas.
| Sistema castellano | cantidades | operación | total en unidades | operación | total en pulgadas | operación | total en metros | ||||||
| varas | 3 | 3 x 40,5 | = | 121,5 | 3 x 3 x 12 | = | 108 | 3 x 3 x 0,279 | = | 2,511 | |||
| pies | 2 | 2 x 13,5 | = | 27 | 2 x 12 | = | 24 | 2 x 0,279 | = | 0,558 | |||
| pulgadas | 1 | 1 x 1,125 | = | 1,125 | 1 x 1 | = | 1 | 1 x 0,279/12 | = | 0,02325 | |||
| líneas | 4 | 4 x 0,09375 | = | 0,375 | 4 x 1/12 | = | 0,333333... | 4 x 0,279/12/12 | = | 0,00775 | |||
| 150 | 133,333333... | 3,10 |
|
|
Esta rejilla de 150 unidades de lado no sólo tutela las operaciones matemáticas que se efectúen en el lienzo de Las Meninas, sino, que además, como módulo regulador, unifica cualquier cálculo en todo sistema conocido de medición.
| 150 unidades | ≡ | 133 y 1/3 pulgadas | ≡ | 3,10 metros |
| 154 unidades | ≡ | 136 y 8/9 pulgadas | ≡ | 3,182666 ... metros |
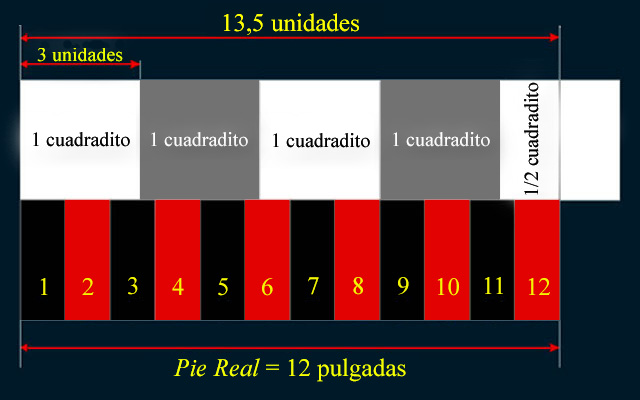
Hablamos, pues, de una rejilla de 50 x 50 cuadraditos de lado que equivale a un gran cuadrado de 3,10 x 3,10 metros, es decir; cada subcuadrado de esta rejilla mide, exactamente, 3 unidades de lado.
 |
|
|
Cuadrícula de trabajo y patrón de medida que acota cualquier detalle de la superficie de Las Meninas.
Si una pulgada equivale a 1,125 unidades en la cuadrícula de trabajo, entonces; sólo hay que multiplicar 1,125 unidades por 12 para obtener 13,5 unidades, que es la cantidad que representa en esta misma cuadrícula 4,5 cuadraditos valiendo el Pie Real 12 pulgadas.
La anchura del Marco de madera del Espejo de Las Meninas mide 13,5 unidades en la rejilla de trabajo.
|
|
|
|
Y el Pie Real, como así lo confirma la pragmática dictada por el monarca Felipe II el 24 de junio de 1568 [11], es el legítimo patrón del sistema de medidas castellano, y en Las Meninas quedó plasmado, pues, en la misma anchura del Marco del Espejo.
|
La cantidad 1,125 unidades por pulgada es el número que traduce las pulgadas castellanas en cualquier clase de sistema de medidas longitudinales, y que, con extrema exactitud, nos pone en contacto directo con las dimensiones reales de Las Meninas. |
 |
|
|
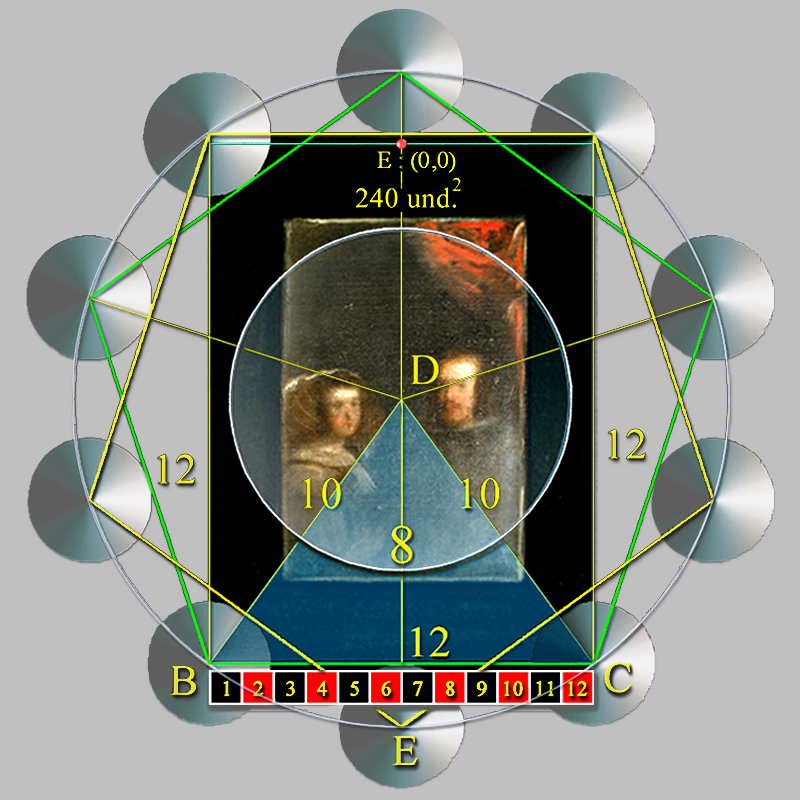
Y no hay ninguna duda, pues, ya que el pentágono y el pentagrama son figuras geométricas que en la Geometría Sagrada simbolizan la proporción divina y la unión entre el mundo terrenal y el divino.
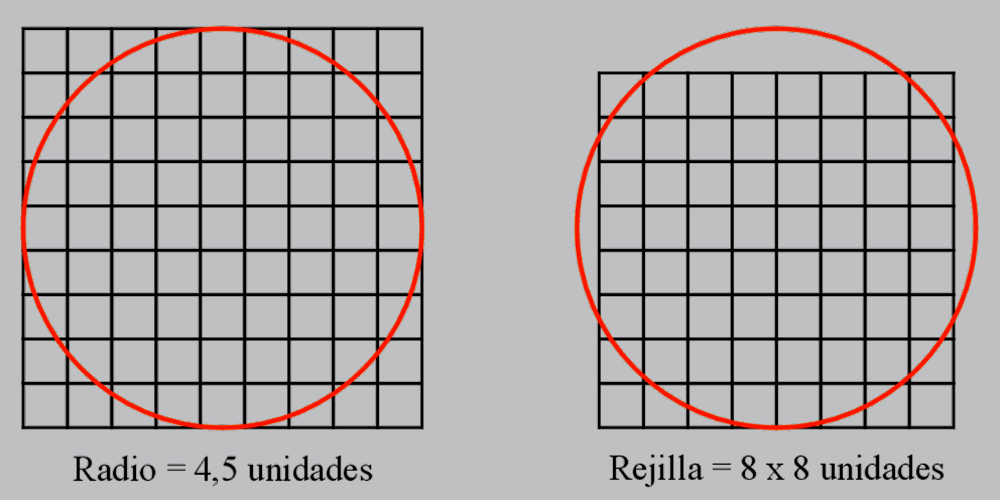
El patrón del sistema de unidades longitudinales que asignamos a la Geometría de la rejilla de trabajo de Las Meninas está presente, pues, en el procedimiento de la demostración de la cuadratura del círculo del Problema 48 del Papiro de Ahmes de 1650 a. c.; una proposición aritmética que consiste en obtener un Cuadrado del mismo área que un Círculo.
 |
|
British Museum de Londres |
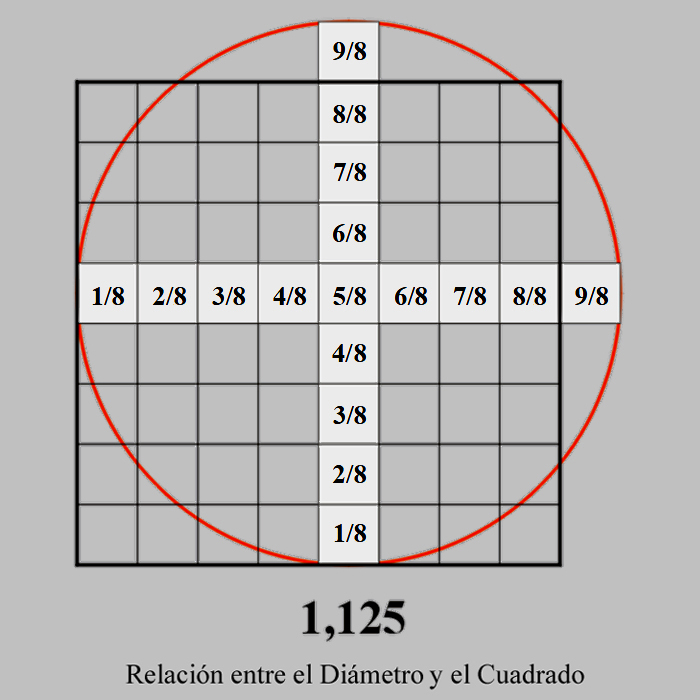 |
El Diámetro de valor 9 y el lado del Cuadrado de 8, están en razón geométrica de 9/8 = 1,125; hablamos, pues, de una proporción sesquioctava, que es aquella que contiene la unidad y un octavo de ella:
|
8/8 + 1/8 = 9/8
1 + 1/8 = 1,125 |
 |
|
|
El escriba Ahmes calcula el área del círculo con un valor de Pi = 256/81 = 3,1605..., y un diámetro igual al lado de 9 unidades del cuadrado circunscrito.
|
OPERACIÓN
π × 4,52
3,1605... × 4,5 × 4,5 = 64 unidades cuadradas |
Y se deduce, pues, que las 64 unidades cuadradas del área del círculo equivalen a una cuadrícula de 8 x 8 unidades de lado, lo que prueba, además, que hace 3600 años la cuadratura del círculo no era una misión imposible.
Más modernamente, en el año 1609, el bachiller Iuan Perez de Moya asevera en su libro ARISMETICA PRACTICA, Y ESPECULATIVA:
El fundamento, o principio de la Ariſmetica, es la vnidad, aſsi como el punto lo es de la Geometria.
1 Pulgada = 0,279 metros / 12 = 0,02325 metros.
| 9 partes | Unidades | La Pulgada en 9 partes | Pulgadas | Milímetros | ||
| 9/8 | = | 1,125 | 9/9 | = | 1 | 23,25 |
| 8/8 | = | 1 | 8/9 | = | 0,888888 | 20,666666 |
| 7/8 | = | 0,875 | 7/9 | = | 0,777777 | 18,083333 |
| 6/8 | = | 0,75 | 6/9 | = | 0,666666 | 15,5 |
| 5/8 | = | 0,625 | 5/9 | = | 0,555555 | 12,916666 |
| 4/8 | = | 0,5 | 4/9 | = | 0,444444 | 10,333333 |
| 3/8 | = | 0,375 | 3/9 | = | 0,333333 | 7,75 |
| 2/8 | = | 0,25 | 2/9 | = | 0,222222 | 5,166666 |
| 1/8 | = | 0,125 | 1/9 | = | 0,111111 | 2,583333 |
|
|
| unidad | pulgada | milímetro |
Y ya que queda entendido que 1,125 unidades equivale a una pulgada castellana, y que la pulgada castellana se divide en doce partes iguales llamadas líneas, señalaríamos, pues, que Diego Velázquez fracciona la pulgada castellana en 9 partes iguales para poder operar con la unidad.
8/9 de pulgada equivale a la unidad en este nuevo plano de Las Meninas.
Hablamos, pues, de una proporción en la que ocho partes de nueve equivalen a la unidad.
No obstante, al número 1,125 habría que considerarle el patrón de la pulgada, ya que es la cantidad reguladora de las unidades geométricas, cuya función práctica no ha variado desde la época de los Sumerios, y, además de ser el número de la proporción que cuadra el círculo con un Pi = 256/81, es también el común dividendo de la pulgada fraccionada en: 9 - 12 - 15 partes iguales en el sistema de medidas castellano.
NÚMEROS DE AQUILES:
72, 108, 200, 288, 392, 432, 500, 648, 675, 800, 864, 968, 972, 1125...
1125 unidades, que le corresponde el valor de 1000 pulgadas, es un número de Aquiles.
Un número natural se llama poderoso cuando todos los exponentes de sus factores primos son mayores o iguales a 2.
Expresado de otra manera:
1125 se descompone en estos dos factores: 32 x 53.
Si N es poderoso, y, un número primo, p, divide a N, entonces p2 también divide a N.
Si 1125 es poderoso, y, un número primo, 3 ó 5, divide a 1125, entonces 32 ó 53 también divide a 1125.
Los divisores del número 1125 son 12:
1, 3, 5, 9, 15, 25, 45, 75, 125, 225, 375, 1125.
Geometría descriptiva - CASO A
Esta obra artística hay que analizarla teniendo en cuenta dos argumentos bien calculados;
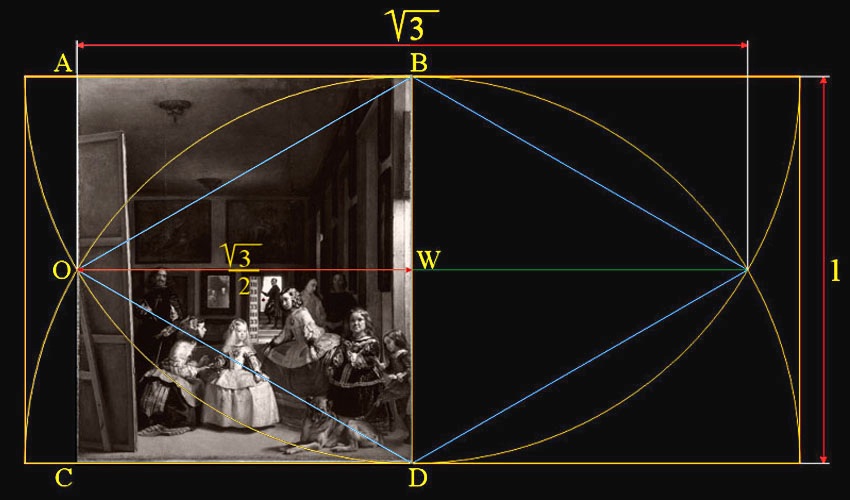
el arranque de esta composición como un espacio cuadrado [12]
y el aspecto final de Las Meninas después de haberse efectuado el estrechamiento por su lateral izquierdo; el lado AC.
Y descubrimos, pues, que la anchura OW de Las Meninas pertenece a la altura del gran triángulo equilátero OBD.
 |
|
|
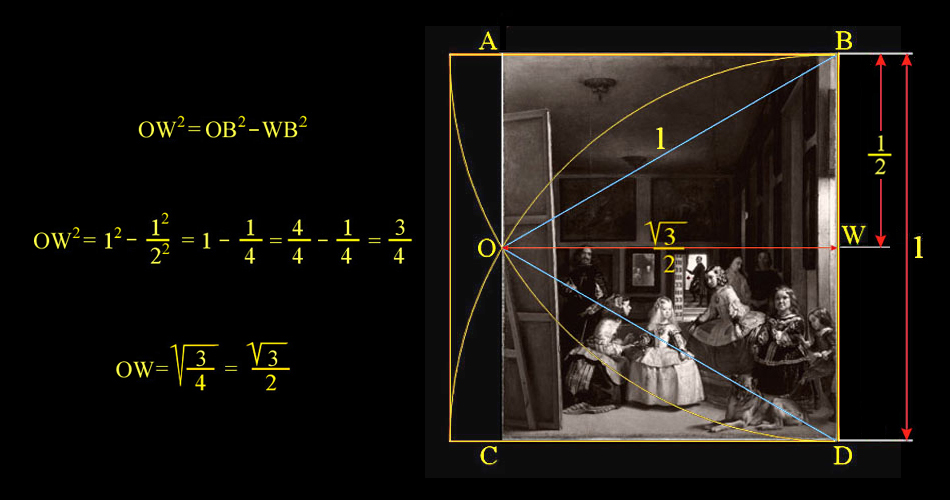
La vesica piscis es un símbolo hecho con dos semicírculos del mismo radio, en este caso el radio equivale a la unidad, de manera que el centro de cada círculo, B y D, está en el perímetro de la circunferencia del otro.
Tenemos que BD = BO = OD = 1
En la antigüedad la razón matemática entre la anchura y la altura de la vesica fue aproximada por el cociente 265/153, que es igual a 1,732026..., y equivalente a √3.
 |
|
|
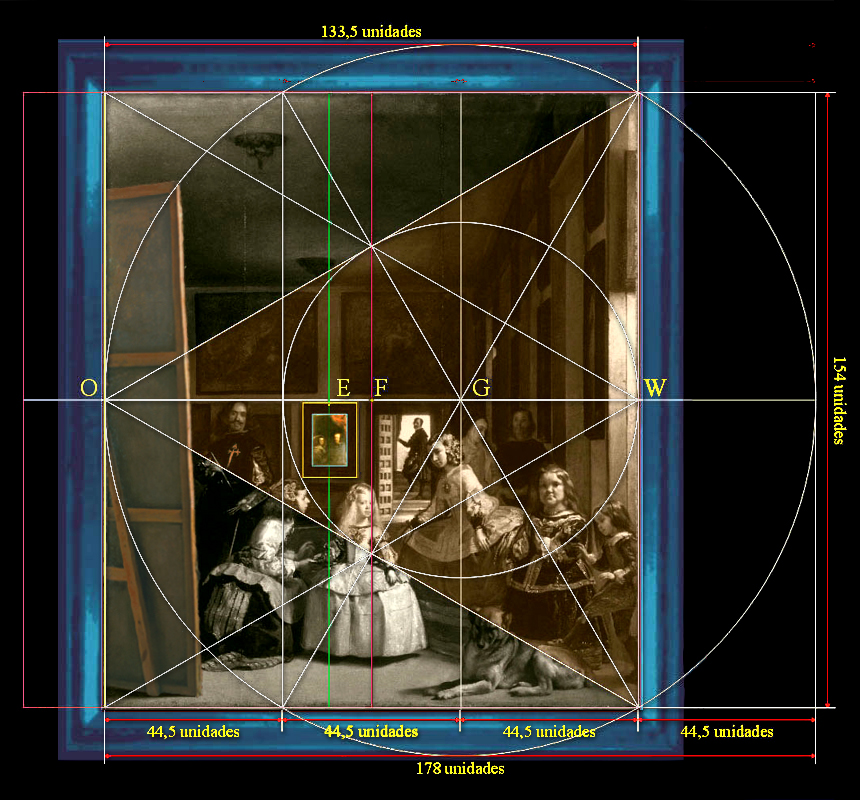
En este CASO A el ratio entre la anchura y la altura de Las Meninas corresponde al cociente 133,5/154, que es igual a 0,866883..., y equivalente a √3/2, que es igual a 0,866025..., cuyas medidas coinciden con las del Catálogo del Museo del Prado.
| Tamaño | Unidades | Sistema castellano | Sistema métrico | Museo del Prado |
| Anchura | 133,5 | 118 pulgadas y 6/9 | 2,759 metros | 2,76 metros |
| Altura | 154 | 136 pulgadas y 8/9 | 3,182666 metros | 3,18 metros |
|
|
 |
|
|
|
Para el estudio de este CASO A hemos partido del enfoque geométrico planteado por Ángel del Campo y Francés en su libro:
La Magia de Las Meninas. Editorial Ediciones Turner - 1985.
De Ángel del Campo utilizamos todo lo que se pudiera aplicar en la construcción de este nuevo esquema de trabajo:
punto de fuga,
nivel de ojos,
y algún que otro dato relativo a la Geometría descriptiva.
Las medidas del lienzo - CASO B
Las Meninas, acotadas por la unión de tres franjas de lienzo de lino que visiblemente componen su anchura, miden 3,18 metros de alto por 2,76 metros de ancho, si bien, habría que detallar oportunamente las características de este lienzo:
|
Esta obra está forrada con el sistema tradicional de la gacha. El soporte original está formado por la unión de tres bandas de lienzo de lino, colocadas verticalmente, es decir, en el sentido de su fabricación; la central y la lateral derecha presentan todo el ancho de la tela, ya que se puede observar el orillo en el borde derecho que dobla sobre el bastidor. La banda lateral izquierda es de menor tamaño y no se observa el orillo; tal vez fue cortada por Velázquez, para conseguir unas determinadas dimensiones en la composición... [13]. |
Dos de las tres bandas de tela que componen el ancho de este lienzo son del mismo tamaño.
|
|
|
|
| Banda izquierda | Banda central | Banda derecha | Anchura total del lienzo |
|
31 pulgadas y 4/9 |
43 pulgadas y 2/3 |
43 pulgadas y 2/3 |
118 pulgadas y 7/9 |
|
0,731083333 metros |
1,01525 metros |
1,01525 metros |
2,761583 metros |
|
|
 |
| Banda izquierda | Banda central | Banda derecha |
Anchura del lienzo original |
|
32 pulgadas y 2/3 |
43 pulgadas y 2/3 |
43 pulgadas y 2/3 |
120 pulgadas |
|
0,7595 metros |
1,01525 metros |
1,01525 metros |
2,79 metros |
|
Aunque es más probable que la anchura de estas tres telas midiesen respectivamente: 32 + 44 + 44 = 120 pulgadas |
El corte vertical por el lado izquierdo del lienzo de Las Meninas supuso un estrechamiento severo respecto a su composición cuadrada inicial, aunque investigarlo es el paso necesario para arribar a otro nivel, y ahondar en la estructura simbólica del tema que tratamos.
Ante estas conclusiones, queda establecida, pues, la cantidad exacta de lienzo que Velázquez dispuso para su labor antes de su montaje en el bastidor original, lo que permite repetir el proceso de preparación con confianza.
Borde del orillo del lino original - CASO C
Con todo, la idea mencionada del tamaño exacto de Las Meninas nos fuerza a experimentar dentro de un cuadrado que mide de lado 155,25 unidades, que equivale a 138 pulgadas y en el sistema métrico a 3,2085 metros, que se extiende hasta lo que hemos dado en llamar:
Borde del orillo del lino original.
Este nuevo planteamiento se basa en la disponibilidad de poder dividir entre dos 138 pulgadas, que es igual a 69 pulgadas, y así deducir dos cuestiones fundamentales al mismo tiempo;
el punto medio de la pared del fondo a 69 pulgadas del Borde del orillo del lino original
y el punto F, correspondiente al punto medio de la creación de Las Meninas.
 |
|
|
El punto F del 1º Caso es el centro inicial del lienzo de Las Meninas.
Es decir:
Horizontal : 10,125 unidades
Vertical : 0,375 unidades
El punto F es un centro secundario, y consecuencia del punto medio del que está tratando realmente Velázquez cuando piensa y medita esta pintura; aunque, como hemos comentado, constituye el eje central de Las Meninas tal cual la contemplamos en el Museo del Prado.
 |
Desglose de la anchura de Las Meninas 2,761583... metros = 133,625 unidades; que equivalen a 118 pulgadas y 7/9.
Es igual a 69 pulgadas = 77,625 unidades.
Es igual a 49 pulgadas y 7/9 = 56 unidades. |
Y entendido que Las Meninas fueron concebidas a partir de un perfecto cuadrado, se deduce que la altura original del lienzo de esta pintura medía el doble del ancho de la distancia entre el centro del espejo y el Borde del orillo del lino original en el canto derecho del moderno bastidor.
69 pulgadas x 2 = 138 pulgadas.
| unidades | pulgadas | metros | medidas castellanas | |
| Altura | 155,25 | 138 | 3,2085 | 138 pulgadas / 12 = 11 pies y medio |
| Anchura | 135 | 120 | 2,79 | 120 pulgadas / 12 = 10 pies |
|
|
La Numerología - CASO D
Y al mismo tiempo, siendo el año 1656 cuando fueron creadas Las Meninas por Diego Velázquez en Madrid, eventualmente, la cifra de este año concuerda, de manera manifiesta, con la misma cantidad de líneas castellanas que hemos asignado a la altura de esta pintura.
Primero observemos los 24 divisores del número 1656:
1, 2, 3, 4, 6, 8, 9, 12, 18, 23, 24, 36, 46, 69, 72, 92, 138, 184, 207, 276, 414, 552, 828, 1656.
Y ahora establezcamos y demos nombre a su valor cuantitativo:
| Sistema castellano | varas | pies | palmos | pulgadas | líneas | puntos | metros | unidades |
| 3 y 10/12 | 11 y 6/12 | 15 y 4/12 | 138 | 1656 | 19872 | 3,2085 | 155,25 |
|
|
Por consiguiente, obtendríamos 138 pulgadas dividiendo 1656 líneas castellanas entre 12, resultado que se haya relacionado, a medida del deseo, con la misma cantidad de pulgadas que las del verdadero tamaño de la altura inicial del lienzo que analizamos.
1656 ÷ 12 = 138.
Y de igual manera la anchura funciona con los mismos guarismos:
1656 ÷ 13,8 = 120.
Las proporciones del tamaño de Las Meninas deducidas por el arquitecto Ramiro Moya nos dan la razón, ya que son exactamente iguales a los resultados que hemos obtenido del estudio de esta misma obra de arte.
En su análisis consideró las siguientes medidas para este lienzo de Diego Velázquez [14].
23K para la altura y 20K para la anchura, valiendo K ≈ 1/2 pie = 0,139 metros.
|
LA ALTURA - 11 pies y medio |
LA ANCHURA - 10 pies |
|||||||||
| Metros | Pulgadas | Unidades | Cuadrícula |
 |
Cuadrícula | Unidades | Pulgadas | Metros | ||
| 3,2085 | 138 | 155,25 | = | 6,75 x 23 | 6,75 x 20 | = | 135 | 120 | 2,79 | |
|
|
Aunque en nuestro caso K valga 0,1395 metros, que equivale a 6 pulgadas, estamos hablando, pues, de las mismas proporciones de este lienzo.
No obstante, el Pie Real mide 0,279 metros, y la anchura de Las Meninas medía 2,79 metros, es decir, diez veces más; por fortuna una relación proporcional exacta [15].
En definitiva, hemos establecido el punto de encuentro entre las distintas equivalencias geométricas, matemáticas y de aritmética castellana del tamaño de Las Meninas.
Las medidas del Inventario de 1834 - CASO E
Existe una histórica y continuada discrepancia a la hora de medir exactamente el lienzo de Las Meninas.
En el Inventario de 1834 del Real Museo de Pinturas, llamado más tarde Museo del Prado, se adjudican al cuadro de Las Meninas las siguientes dimensiones:
|
La Ynfanta Da Margarita Maria de Austria, hija de Felipe 4o á quien sus damas presentan para vever agua un búcaro (uno de los mas hermosos cuadros del autor). Velazquez. 12,1 x 10,7 Lo Palma 1.100 / 400.000 |
Las medidas del Inventario de 1834 no corresponden a las dimensiones actuales porque esta pintura se mide con marco.
Veamos:
Medidas del Inventario del año 1834: 12,1 x 10,7.
Estas medidas castellanas corresponden a:
12 pies y 1 pulgada x 10 pies y 7 pulgadas = 145 pulgadas x 127 pulgadas.
 |
Ahora restaremos 7 pulgadas del marco, del alto y ancho, de esta pintura:
145 pulgadas - 7 pulgadas = 138 pulgadas.
127 pulgadas - 7 pulgadas = 120 pulgadas.
Por lo que el ancho del marco medía 3 pulgadas y 1/2.
3,5 pulgadas x 0,02325 metros por pulgada = 0,081375 metros = 8,1375 centímetros.
La proporción - CASO F
El tamaño del lienzo de
Las Meninas, o
cualquier retrato u objeto pintado de esta bella pintura, depende íntegramente de las
proporciones regulares.
Partimos de las medidas, de la altura y anchura del lienzo original de Las Meninas, que ya han sido consideradas en el apartado anterior:
| unidades | pulgadas | metros | medidas castellanas | |
| Altura | 155,25 | 138 | 3,2085 | 138 pulgadas / 12 = 11 pies y medio |
| Anchura | 135 | 120 | 2,79 | 120 pulgadas / 12 = 10 pies |
|
|
La anchura de Las Meninas mide 120 pulgadas
Factorización de 2 x 2 x 2 x 3 x 5 = 120.
Los divisores del número 120 son 16:
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120.
La altura de Las Meninas mide 138 pulgadas
Factorización de 2 x 3 x 23 = 138.
Los divisores del número 138 son 8:
1, 2, 3, 6, 23, 46, 69, 138.
| LA ALTURA | LA ANCHURA | |||||||||||
| Metros | Pulgadas | Unidades | Cuadrícula |
 |
Cuadrícula | Unidades | Pulgadas | Metros | ||||
| 3,2085 | 138 | 155,25 | = | 155,25 x 1 | 135 x 1 | = | 135 | 120 | 2,79 | |||
| 67,5 x 2 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 77,625 x 2 | 45 x 3 | = | 135 | 120 | 2,79 | |||
| 33,75 x 4 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 51,75 x 3 | 27 x 5 | = | 135 | 120 | 2,79 | |||
| 22,5 x 6 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 25,875 x 6 | 16,875 x 8 | = | 135 | 120 | 2,79 | |||
| 13,5 x 10 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 6,75 x 23 | 11,25 x 12 | = | 135 | 120 | 2,79 | |||
| 9 x 15 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 3,375 x 46 | 6,75 x 20 | = | 135 | 120 | 2,79 | |||
| 5,625 x 24 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 2,25 x 69 | 4,5 x 30 | = | 135 | 120 | 2,79 | |||
| 3,375 x 40 | = | 135 | 120 | 2,79 | ||||||||
| 3,2085 | 138 | 155,25 | = | 1,125 x 138 | 2,25 x 60 | = | 135 | 120 | 2,79 | |||
| 1,125 x 120 | = | 135 | 120 | 2,79 | ||||||||
|
|
Y tal y como se ha probado, los tamaños de la altura y anchura del lienzo original de Las Meninas miden;
138 pulgadas para la altura,
y para la anchura 120 pulgadas.
Cantidades que, en definitiva, resultan de la medición del tamaño de la anchura y altura del lienzo original de Las Meninas en pulgadas castellanas, y que corresponden a dos números concretos localizados en las ternas de la escuadra perfecta de Pitágoras.
| Cateto menor | Cateto mayor | Hipotenusa |
| 3 | 4 | 5 |
| 90 | 120 | 150 |
| 120 | 160 | 200 |
| 103,5 | 138 | 172,5 |
| 138 | 184 | 230 |
|
|
Pero, siempre, con la precaución que requiere estos casos tan especiales:
120 pulgadas x 138 pulgadas = 16.560 pulgadas cuadradas.
Que representan diez veces al número 1656, que es el año de este cuadro.
La rejilla de 152 unidades
La máxima rejilla geométrica que proponemos mide 152 x 152 unidades, que se extiende hasta lo que hemos dado en llamar:
Límite de la rejilla de 152 unidades.
152 unidades equivalen a 3,141333... metros, es decir; 135 pulgadas y 1/9.
Esta cuadrícula hace posible trabajar holgadamente sobre la superficie pictórica de Las Meninas, porque es cierto que la altura actual de 3,18 metros menos 3,141333... metros del lado de la rejilla geométrica de 152 unidades, dan un margen de 0,038666... metros.
Tendremos en cuenta, pues, que Las Meninas cambiaron de formato a partir de su reentelado, por lo que actualmente el lienzo original está pegado a un lienzo más moderno, de manera, que alrededor del perímetro de este óleo existe un área sin pintura, que Velázquez nunca quiso mostrar porque doblaba sobre el canto de la madera del bastidor original.
|
|
|
|
Para ser más exactos notificaremos:
|
| unidades | medidas castellanas | metros | |
| Margen superior | 2 | 1 pulgada y 7/9 | 0,041333... |
| Límite de la rejilla de 152 unidades | 152 | 135 pulgadas y 1/9 | 3,141333... |
| Margen inferior | 1,25 | 1 pulgada y 1/9 | 0,025833... |
| Borde del orillo del lino original | 155,25 | 138 pulgadas | 3,2085 |
| Suelo | 157,5 | 140 pulgadas | 3,255 |
|
|
|
|
|
|
Como hemos ya documentado, la altura inicial de Las Meninas era de 3,2085 metros, que corresponden al tamaño del lado del formato cuadrado que denominamos Borde del orillo del lino original.
En definitiva, al menos 0,027125 metros de tela original faltan en la parte inferior de la altura.
3,2085 - 3,181375 = 0,027125 metros.
No obstante, la toma de contacto con el cuadrado de 152 unidades de lado nos ha dirigido hacia una seria propuesta.
|
Sistema de medidas |
Anchura |
|
Altura |
|
Total de Coordenadas |
|
metros |
3,141333... |
x |
3,141333... |
|
|
|
unidades |
152 |
x |
152 |
= |
23.104 |
|
|
La rejilla de 152 unidades garantiza, pues, el espacio de trabajo que hace viable representar la Geometría áurea, y adecuar, en un mapa de coordenadas de 23.104 posiciones posibles, a las diez esferas cabalistas en el transparente aire de la sala del Alcázar de Madrid representada en este óleo.
La altura de trabajo
La altura pictórica de
3,2085
metros, y equivalente a
138 pulgadas, la
hemos considerado teniendo en cuenta dos factores:
Que la acotación del borde del larguero superior estuviera promediado con el inferior,
y que la cuadrícula que denominamos Borde del orillo del lino original solapase sobre el orillo del lateral derecho.
|
|
|
Sin embargo, la otra altura de 3,181375 metros podríamos considerarla como el tamaño actual del lienzo, pero que ciñéndonos al Catálogo del Museo del Prado correspondería a 3,18 metros.
Características de la altura de 3,181375 metros:
Que equivaliera en el sistema de medidas castellano lo más aproximado a 3,18 metros,
y que esta altura se ajustase al tamaño de las rejillas de trabajo centradas en la coordenada [0,0], y así reanimar de nuevo la completa experiencia creativa de Las Meninas.
| Catálogo del Museo del Prado | Sistema métrico | Medidas castellanas | Unidades de trabajo | |
| Altura | 3,18 metros | 3,181375 metros | 136 pulgadas y 10/12 | 153,9375 |
| Anchura | 2,76 metros | 2,761583... metros | 118 pulgadas y 7/9 | 133,625 |
|
|
|
|
|
|
| metros | pulgadas | medidas castellanas | unidades | |
| Altura | 3,2085 | 138 | 138 pulgadas / 12 = 11 pies y medio | 155,25 |
| Anchura | 2,79 | 120 | 120 pulgadas / 12 = 10 pies | 135 |
|
|
Analizaremos, pues, las nuevas medidas que ofrece el Museo del Prado del tamaño de Las Meninas, que, aunque este lienzo haya crecido unos pocos centímetros, está sujeto a un sistema de medidas basado en reglas de Geometría que no permite errores de medición.
Es decir; para medir el lienzo de esta obra maestra hay que utilizar un modelo matemático exacto, ya que consideramos que el cálculo de estas nuevas medidas asignadas a esta pintura no está bien determinado.
Para la altura se usa un valor del pie conveniente: 3,205 metros / 11,5 pies = 0,278695... metros por pie castellano.
Para la anchura se usa un valor del pie casi conveniente: 2,815 metros / 10 pies = 0,2815 metros por pie castellano.
Una diferencia de medición en el tamaño del pie de 2,805 milímetros.
| Siglo XX | Museo del Prado año 2021 | Medidas castellanas | Unidades de trabajo | |||||
| Altura | 3,18 metros | 3,205 metros | = | 137,849462... pulgadas | ~ | 137 pulgadas y 10/12 | ~ | 155,0625 |
| Anchura | 2,76 metros | 2,815 metros | = | 121,075268... pulgadas | ~ | 121 pulgadas y 1/12 | ~ | 136,21875 |
|
|
Aunque habría que añadir que Pedro de Madrazo, en el Catálogo del Museo del Prado publicado en 1872, señala que el lienzo de Las Meninas mide:
Alto: 3,18 m.
Ancho: 2,76 m.
Y estas medidas se han mantenido, sin ninguna duda, durante 150 años.
En la siguiente imagen se aprecia, pues, lo que falta del lienzo original:
|
|
| Medidas castellanas | ||
| Altura | Anchura | |
| 11 pies y medio | 10 pies | |
Luego, deducida la cantidad necesaria de lienzo, que utilizó el artista para diseñar su gran obra, abordaremos otras cuestiones menos terrenales, pero, eso sí, igual de exactas.
Este tema en concreto será la base geométrica de lo que analicemos a continuación.
notas a pie de página
1 - La unidad queda dividida gráficamente en 10.000 partes; y la superficie de la foto de Las Meninas mide: 133,6250 unidades por 153,9375 unidades.
Operaremos de la siguiente manera; primero multiplicaremos a ambas cantidades por 10.000, y después a estos dos resultados obtenidos los multiplicaremos de nuevo entre sí para calcular los puntos cartesianos localizados sobre la superficie de este plano.
Es decir; hemos dividido la imagen de Las Meninas en 11336.250, un millón trescientos treinta y seis mil doscientos cincuenta posibles abscisas horizontales, por 11539.375, un millón quinientos treinta y nueve mil trescientos setenta y cinco posibles ordenadas verticales, para calcular los resultados que aportamos.
Hablaríamos de esta posible gran cantidad de puntos localizados sobre el óleo de Las Meninas:
22056.98911843.750.
2 - El micrómetro es la unidad de longitud equivalente a una millonésima parte de un metro.
Se abrevia µm, y es también conocido como micra, abreviado µ.
3 - Las Meninas en una antigua restauración fueron reenteladas, lo que supone que el lienzo original de esta pintura está actualmente pegado a un nuevo lienzo, de modo, que alrededor de todo su perímetro existe un área de lienzo sin pintura, que Velázquez nunca quiso mostrar, porque doblaba sobre el bastidor original.
Una de las características más importante del reentelado, o forración definitiva, es el de acompañarle un nuevo formato, preciso y meditado, determinado por el restaurador, aunque tuvo como resultado, como hemos ya apuntado, el de alterar el tamaño de Las Meninas.
|
|
|
|
Carmen Garrido Pérez puntualiza en su libro, VELÁZQUEZ, TÉCNICA Y EVOLUCIÓN, MUSEO DEL PRADO, algo más sobre esta misma cuestión:
|
En el borde inferior, por el anverso de la pintura son visibles los agujeros dejados por los clavos de sujeción del soporte a un bastidor antiguo. En el borde superior también se observan marcas del mismo tipo producidas por el mismo hecho. |
En la restauración de Las Hilanderas, también obra de Velázquez, se constató, según las marcas visibles radiográficas, que los listones de madera del bastidor original medían de ancho entre 3 y 4 centímetros.
4 - En el Sefer Yetzirah, cuyo texto es el tratado más antiguo del mundo contemplativo hebreo, se describe el proceso cosmogónico mediante la combinación de letras hebreas; letras que equivalen a los ladrillos de los que se sirve el Arquitecto Divino para la construcción del mundo.
En el Tomo I / Página 151: OEDIPVS AEGYPTIACVS - ATHANASII KIRCHERI - ROMAE. MDCLII. Libro dedicado al emperador Fernando III, el padre de la reina de España, Mariana de Austria, es decir; el suegro y cuñado del rey Felipe IV, Athanasius Kircher lo menciona con el nombre R. Abraham in Iethſira.
|
Hinc in arbore Sephiroth apud Cabaliſtas גמדות ſeu tres proprietates Deo affinguntur, quibus Deum omnia feciſſe memorant, ſuntque . בִּינָה . חָכְמָה . כֶּתֶר Corona, Sapientia, Intelligentia; quas R. Abraham in Iethſira appellat מספר ספר סופר id eſt, numerantem, numerum, & numeratum; quae tria exacte reſpondent tribus ſupra a Iamblicho citatis nominibus, Amun, Phtha, Emepht. |
La fecha de composición de este texto es causa de debate; la mayoría de los entendidos están de acuerdo en que fue escrito o compilado entre el siglo II y VI, sin embargo, Steven M. Wasserstrom ha señalado de una clara transición islámica en el siglo IX, aunque es del todo seguro que ejerció una gran influencia especulativa y mística durante el siglo X.
De acuerdo a Ithamar Gruenwald hay tres primeras versiones del Sefer Yetzirah; una corta, otra larga de algo menos de 2500 palabras, y la llamada versión Saadia con comentarios del temprano siglo X.
5 - Nobleza del Andaluzia de Gonzalo Argote de Molina. Sevilla. 1588.
Página 112 - Libro Primero - De la Svcession de los Caſtros en la Caſa Real; y de los linages que vſan en Caſtilla de la Deviſa de los Roeles. Cap. CIII.
6 - En 1984, el entonces director del Prado, Alfonso E. Pérez Sánchez documenta en el Boletín del Museo del Prado:
El día 14 de mayo se inició, por mano de John Brealey, Director del Departamento de Conservación de Pinturas del Museo Metropolitano de Nueva York, la limpieza de Las Meninas, gracias a la generosa ayuda de Mrs. Hilly Mendelssohn, que había donado al Museo del Prado una importante suma de dinero para que fuese aplicada a la restauración de alguna obra significativa.
Las Meninas, una vez restauradas, fueron expuestas de nuevo al público el 31 de julio de 1984, y, como suele suceder en estos casos, se desató la polémica, algo se había perdido en la limpieza; rancios barnices repintados, luces opacas...
7 - Las Meninas fueron científicamente examinadas por el Gabinete de Documentación Técnica del Museo del Prado, que realizó un amplio estudio ayudado por; radiografías, reflectografías infrarrojas, fluorescencias ultravioleta, fotografías de técnicas diversas, análisis de pigmentos y soportes, etc.
Esta metodología es la habitual en la restauración de un cuadro.
8 - Es evidente que Las Meninas no es un cuadro cuadrado, pero plantearemos el concepto del cuadrado como proporción inicial para el estudio consecuente de su formato actual.
Una vez dispuestos los útiles necesarios, analizaremos el corte vertical del lado izquierdo del óleo de Las Meninas, y, como se puede comprobar en la siguiente ilustración, nos hemos decantado por una condición geométrica totalmente nueva, pero viable de llevar a cabo por el pintor Diego Velázquez.
 |
Límite
de la rejilla de 152 unidades
La Rejilla de 152 unidades y los 10 Sefirot + Dahat en el espacio pictórico de Las Meninas
Cada unidad en el plano que presentamos equivale a 8/9 de pulgada, que traducido al sistema métrico equivale a:
El Pie Real de 0,279 metros dividido entre doce es igual a 0,02325 metros la pulgada, este resultado, a su vez, lo dividimos entre 9, que nos da como resultado 0,002583333 metros ó 1/9 de pulgada.
La solución de la equivalencia de 8/9 de pulgada en el sistema métrico será por tanto la multiplicación de 0,002583333 metros por 8, que es igual a 0,020666666 metros.
Más o menos 2 centímetros.
Si una pulgada vale 0,02325 metros y equivale a -------------------------- 1,125 unidades.
8/9 de pulgada que es igual a 0,020666666 metros equivaldrá a ------------------ X unidades.
Hagamos esta simple regla de tres:
0,020666666 metros x 1,125 unidades por pulgada / 0,02325 metros por pulgada = 1 unidad.
Continuemos con la cuestión matemática, y calculemos, ahora, el número necesario de cuadrados de 19 x 19 unidades que hacen falta para cubrir a todo el lienzo, y así componer de nuevo, perfectamente, la obra artística de Velázquez.
Como observamos ocho cuadrados han sido desestimados, siendo el total de cuadrados usados en la composición artística de 56.
Estudio del Corte vertical del lado izquierdo en la Rejilla de 64 cuadrados - Límite de la rejilla de 152 unidades.
Esta magnífica rejilla que contemplamos consta de 64 cuadrados de 19 x 19 unidades cada uno, y mide 152 unidades de lado.
Entendida la imagen anterior observamos; primero que una banda de ocho cuadrados de la rejilla no cubre a Las Meninas, y segundo; que en tal caso analizaremos la porción de rejilla que sí cubre y acota la anchura de esta pintura.
La anchura que cubre el Límite de la rejilla de 152 unidades.
Vemos que son 7 cuadrados de 19 unidades de lado los que cubren apropiadamente la anchura de Las Meninas. A continuación averigüemos a que equivale en metros 7 cuadrados de 19 unidades de lado.
Primero conozcamos que: 7 x 19 unidades = 133 unidades.
Cálculo directo
Quedaría así: 133 unidades / 1,125 unidades por pulgada = 118,222222222 pulgadas.
Que equivale a; 118,222222222 pulgadas x 0,02325 metros por pulgada = 2,748666666 metros.
Esta cantidad hace posible, aunque Las Meninas midan de ancho 2,76 metros, trabajar holgadamente sobre una superficie pictórica cuyo lienzo ha de doblar sobre su bastidor para ser sujetado con clavos.
La altura que cubre el Límite de la rejilla de 152 unidades.
Vemos que son 8 cuadrados de 19 unidades los que cubren apropiadamente la altura de Las Meninas.
19 unidades x 8 = 152 unidades, que equivalen a 135 pulgadas y un 1/9.
Cálculo indirecto
El desglose de la cantidad de 135 pulgadas y un 1/9 se llevaría a cabo de la siguiente manera:
Un pie Real equivale a 12 pulgadas, y en nuestros tiempos a 0,279 metros.
Hagamos la operación siguiente: 0,279/12 = 0,02325 metros, esta cantidad en metros es la equivalencia de lo que valía una pulgada castellana en la época de Velázquez.
0,02325/9 = 0,002583333 metros, este resultado representa 1/9 de pulgada, o sea, 2 milímetros y medio...
Ahora multiplicaremos y sumaremos adecuadamente: 135 x 0,02325 = 3,13875 metros, más 0,002583333 metros, que es el valor 1/9 de pulgada.
Que quedaría finalmente así: 3,13875 + 0,002583333 = 3,141333333 metros.
Esta cantidad hace posible, aunque Las Meninas midan de alto 3,18 metros, trabajar holgadamente sobre una superficie pictórica cuyo lienzo ha de doblar sobre su bastidor para ser sujetado con clavos.
Conclusión
Hablamos, pues, del análisis y aplicación de las medidas concretas de la rejilla que hemos denominado: Límite de la rejilla de 152 unidades.
Estos resultados obtenidos son la máxima lectura geométrica, manteniendo el punto E como centro de coordenadas, X = 0 e Y = 0, sobre la altura y la anchura del lienzo de Las Meninas.
El punto E se aloja en la parte superior del marco del espejo con los reyes de España reflejados en su interior.
9 - Vitrubio, en su libro Los Diez Libros de Arquitectura, en el Libro Primero Capítulo II nos aconseja:
La simetría o proporción es una concordancia uniforme entre la obra entera y sus miembros, y una correspondencia de cada una de las partes separadamente con toda la obra. Porque así como en el cuerpo humano hay una proporción y una simetría entre el codo, el pie, la palma de la mano, el dedo y las restantes partes, ocurre igual en toda construcción perfecta.
Marco Lucio Vitrubio, Los Diez Libros de Arquitectura, traducción por Agustín Blánquez, Editorial Iberia, S. A. - Barcelona, 1980.
10 - En el museo National Gallery de Londres se halla la tabla: Los desposorios de los Arnolfini, firmada en el año 1434 por Jan Van Eyck; 1390-1441.
Esta obra de Van Eyck aparece en el Inventario del año 1789 en el Palacio Real de Madrid, aunque, más tarde, fue robada por un general de Napoleón a principio del siglo XIX.
Recordaríamos con este dato que esta pequeña Obra Maestra, de 81,8 cm. por 59,7 cm., se encontraba en el siglo XVII en la completísima colección de pintura del rey Felipe IV.
11 - En el año 1567, y tras el fracaso del Ordenamiento de Montalvo iniciado por los Reyes Católicos en 1484, Felipe II promulga el Código conocido como Nueva Recopilación de las Leyes de España, mediante el cual intenta acabar con el caos legislativo existente.
Dentro de este Código recopilado por las Cortes de Valladolid y Madrid a partir de 1523; de las Leyes del Fuero Real, las 18 Leyes de Toro, el Ordenamiento de Alcántara y el de Montalvo, se enmarca la pragmática dictada por el propio monarca desde El Escorial el 24 de junio de 1568:
Y otroſi, que el paño y lienço y ſayal, y las otras coſas que ſe venden a varas, que ſe vendan por la vara Caſtellana: y en cada vara, que den una pulgada al traues, y que se midan el paño por eſquina: y declaramos que la vara Caſtellana de que ſe ha de vſar en todos eſtos Reynos, ſea la que hay y tiene la ciudad de Burgos.
Libro quinto - Titulo XIII. RECOPILACION de las Leyes deſtos Reynos, hecha por mandado de la Mageſtad Catholica del Rey don Philippe Segundo nuestro Señor. Alcala de Henares, en casa de Iuan Iñiguez de Liquerica impreſſor de libros. Año M.D.LXXXI.
La Vara Castellana, que equivale a tres pies, será la que justifique la indudable relación entre la base geométrica y la Aritmética.
|
|
pies |
pulgadas |
unidades |
metros |
|
Vara Castellana |
3 |
36 |
40,5 |
0,837 |
|
|
Es de señalar que para la elaboración de todos los cálculos aritméticos y geométricos hemos usado el valor de un pie Real a 0,279 m.
La medida más extendida era la vara de Burgos o de Castilla con un pie de 0,2786 m, difundida por veinticinco provincias, pero dándose singularidades como la de Madrid con su pie de 0,281 m.
Esta diferencia de 2 mm., respecto al tamaño del pie castellano de Madrid, no supone ningún error, ya que entendemos que el tamaño de un pie Real a 0,279 m. escala las medidas geométricas longitudinales y proporcionales con una equivalencia métrica más exacta.
12 - En este análisis, invariablemente, estudiamos esta composición iniciada a partir de un cuadrado perfecto.
13 - Boletín del Museo del Prado. Mayo-agosto 1984. La restauración de Las Meninas de Velázquez. Manuela B. Mena Marqués.
14 - Ramiro Moya: El trazado regulador y la perspectiva en Las Meninas. REVISTA ARQUITECTURA. AÑO 3 NUM. 25 - ENERO 1961.
|
|
|
|
15 - Los únicos números a tratar en Las Meninas estarían ya resueltos en el trazado primoroso de una impecable cuadrícula sobre el lienzo.
John F. Moffit puntualiza sobre este lienzo:
|
El encuadre arquitectónico de Las Meninas, identificado en nuestra ya publicada investigación, fue recreado con absoluta precisión, y por ello, e indudablemente, con la ayuda de algún tipo de ingenio mecánico. De acuerdo con ello, como nosotros creemos ( y la prueba absoluta probablemente requeriría raspar el cuadro hasta la preparación ) , Velázquez debió de cubrir primeramente el lienzo con un sistema lineal o de rejilla ( probablemente impuesto sobre la superficie con finas líneas de carboncillo ) y casi con seguridad con retículas individuales de ½ o un pie para cada subcuadrado ( 1 pie = 1/3 de vara = 0,278 metros ) . Esta retícula correspondería a la plantilla de la pantalla cuadriculada de tamaño reducido, que utilizaban tradicionalmente los pintores, el marco de perspectiva, esto es, “el velo” descrito primeramente por León Battista Alberti ( en su Della Pintura, libro que estaba en la biblioteca de Velázquez ) . Dados algunos precedentes históricos y físicos, casi con seguridad esta retícula pudo ser grabada en la placa visual de una cámara oscura. |
Página 182 - Anatomía de Las Meninas; realidad, ciencia y arquitectura. Boletín del Museo del Prado. Septiembre-Diciembre 1986.
Según los cálculos de John F. Moffit media vara mediría 0,4175 metros, en nuestra investigación: 0,4185 metros.
En este nuevo plano 3 unidades es el equivalente al lado de cada uno de los cuadraditos que usamos, y miden el resultado de dividir 3,10 metros, la altura de la rejilla de 150 unidades, entre 50 cuadraditos, es decir; 0,062 metros; lo que representaría que cada cuadradito mediría, entonces, 2 pulgadas y 2/3.
Comprobación:
Por ajuste matemático damos al pie castellano el valor de 0,279 metros.
Si un Pie Real, que son 12 pulgadas, equivale a 0,279 metros, 0,062 metros equivaldrá al resultado que buscamos.
| 12 pulgadas |
0,279 metros |
|
2,666666666 pulgadas equivale a 2 pulgadas y 2/3 |
0,062 metros |
Si dividimos 0,4175 entre 0,062 obtenemos el resultado de 6,733870967..., es decir; que esta nueva cuadrícula sobre Las Meninas propone una retícula individual para cada subcuadrado 6,733870967... veces más pequeña que la de John F. Moffit.
Si elegimos la otra medida de 1 pie = 1/3 de vara = 0,278 metros, obtendríamos una retícula individual para cada subcuadrado 4,483870967... veces más pequeña que la de Moffit.
La división del Pie Real castellano
La base geométrica de esta investigación está sustentada por la perfecta relación entre el antiguo sistema castellano y el actual sistema métrico.
| Sistema castellano | vara | pie | palmo | pulgada | línea | punto | milímetros | unidades |
| vara | 1 | 3 | 4 | 36 | 432 | 5184 | 837 | 40,5 |
| pie | 1 | 3/4 | 12 | 144 | 1728 | 279 | 13,5 | |
| palmo | 1 | 9 | 108 | 1296 | 209,25 | 10,125 | ||
| pulgada | 1 | 12 | 144 | 23,25 | 1,125 | |||
| línea | 1 | 12 | 1,9375 | 0,09375 | ||||
| punto | 1 | 0,16145833 | 0,0078125 |
|
|
| unidad | pulgada | milímetro |
|
INICIO |
|
Aplicación del Pie Real |
|
El Árbol de la Vida |
|
El Escudo de Armas |
La Escalera |
La Perspectiva |
La Pared del fondo |
El Espejo |
|
|
La Herencia |
|
La Sagrada Simbología |
|
|
La Astrología |
Buena medición |
La Paleta del pintor |
Los Planos |
La Divina Proporción |
|
|
El color del Aire |
|
La Puerta |
|
|
Acotación |
La Paz de los Pirineos |
La Perspectiva de la Puerta |
La Infanta Margarita |
El Teorema de Pitágoras |
|
|
Coordenadas |
|
El Corazón |
|
|
La Espiral |
|
El Centro |
|
El Bastidor |
|
Marian de Austria |
Braccio fiorentino |
|
|