[ resolución gráfica 1920 X 1080 ]

Centro de coordenadas

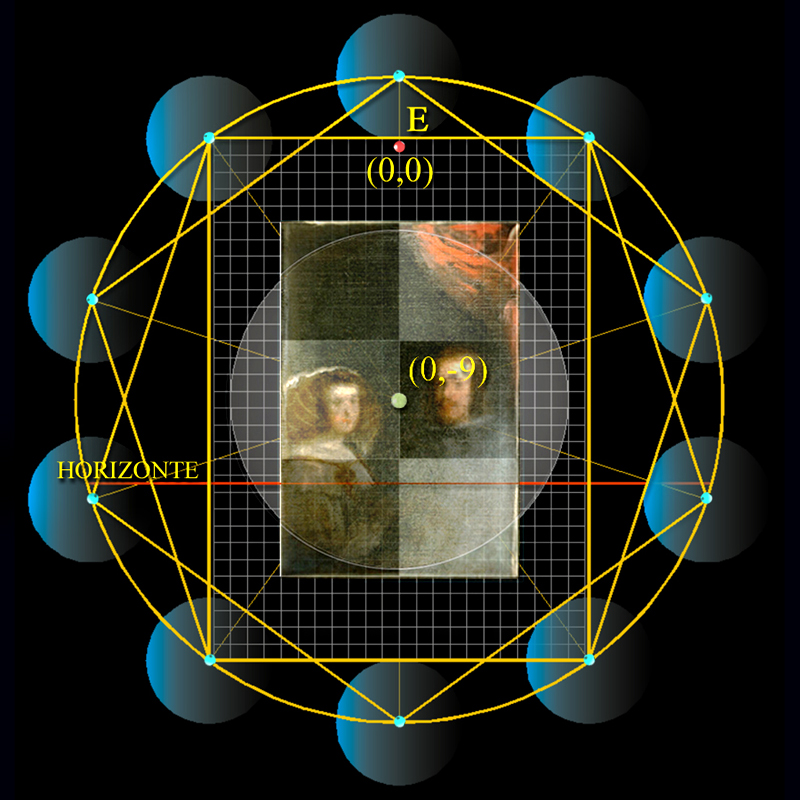
El Espejo de Las Meninas está concebido, pues, a partir de la figura de un decágono compuesto por dos pentágonos superpuestos, en el que cuatro de sus vértices determinan, óptimamente, los límites del ancho y alto del marco de madera que lo rodea.

De modo, que a partir de este esquema, Velázquez disponía en el Espejo a la Sefira nº 9, Yesod, el Fundamento, donde el rey Felipe IV y la reina Mariana de Austria refrendan, desde entonces, una Alianza divina.

El centro de coordenadas, [0, 0], está situado, pues, en el punto E en la parte superior de la moldura del Espejo.

CENTRO DE COORDENADAS

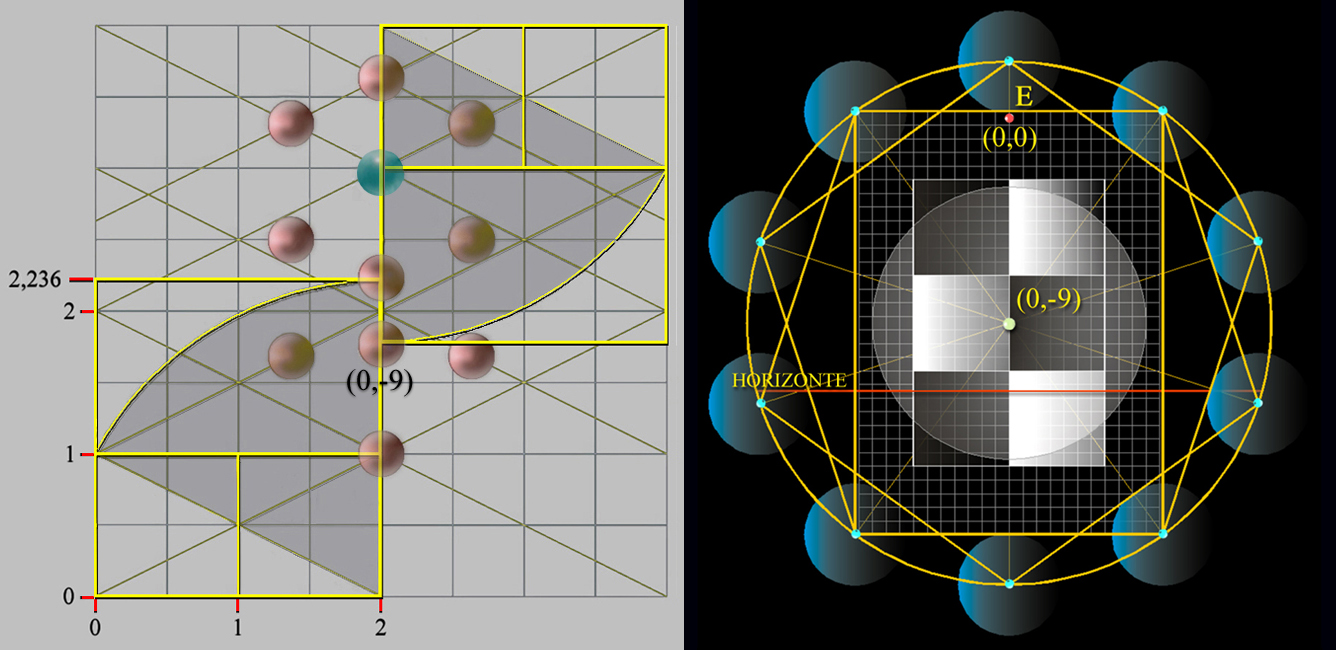
Esencialmente, el Axis Mundi, el portal que conecta el Cielo y la Tierra, se le denomina el Centro del Mundo, y, como centro sagrado, en él convergen religión y mitología.

El Axis Mundi es también conocido como el eje, pilar, columna, árbol, centro cósmico del Mundo, el punto de conexión entre el cielo y la tierra, donde todas las direcciones de la brújula se encuentran.

En definitiva, el centro geométrico del espacio de Las Meninas está inspirado en un tipo de creencia espiritual vinculada con lo sobrenatural.

MACRO & MICROCOSMO

Tamaños de las cuadrículas

Aunque el lienzo de Las Meninas no tenga forma cuadrada plantearemos el concepto del cuadrado como proporción inicial del estudio de su formato actual, y el consecuente análisis de su velada e importante simbología.

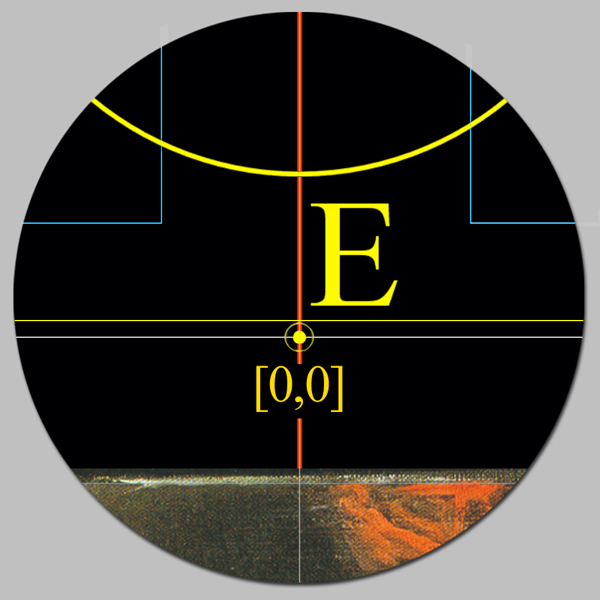Las cuadrículas de trabajo sobre la superficie de Las Meninas se subordinan al sistema de medidas castellanas y a coordenadas cartesianas, y se sustentan, pues, como centro de este plano, en el punto E situado en la parte superior del espejo.

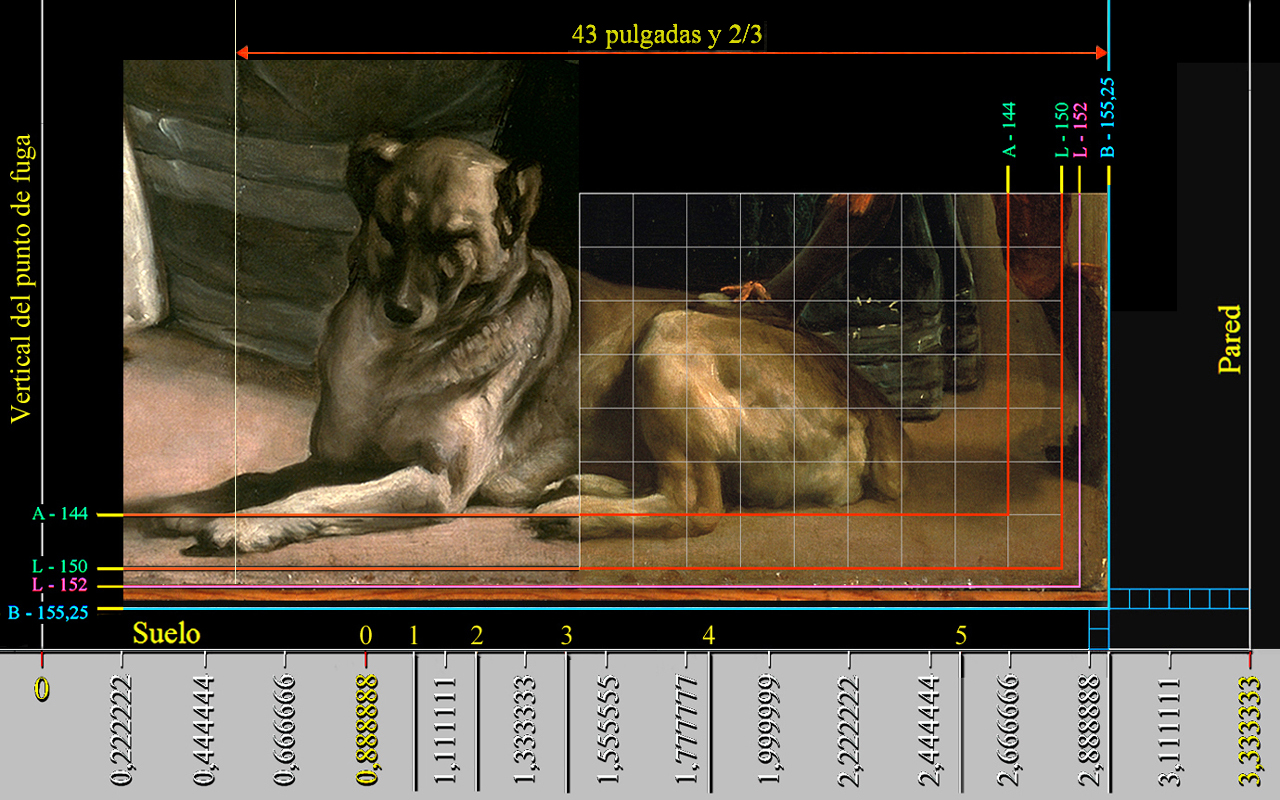
Tipos de cuadrículas sobre la superficie de Las Meninas:

La primera es Línea de acotación, de 144 unidades de lado, que regula el tamaño de la anchura exacta de la pared del fondo, y colabora en la localización de las dos esquinas inferiores de esta misma pared.
La segunda es la cuadrícula de 50 cuadraditos de lado, Límite de la rejilla de 150 unidades, que ha sido el medio imprescindible para recuperar del olvido las antiguas medidas castellanas.
La tercera la denominamos Límite de la rejilla de 152 unidades, que es la que delimita el tamaño de la anchura y altura de la labor geométrica de este lienzo, y sitúa, correctamente, las diez esferas cabalísticas en este espacio aéreo.
Y la cuarta corresponde al Borde del orillo del lino original, que es la que limita el perímetro, o borde del lienzo de Las Meninas, a partir del orillo de su lateral derecho, antes de ser montado y clavado a su bastidor original.
Y a la derecha el canto de la nueva tela de forración clavada al moderno bastidor.

Modelo	Acotación geométrica	Unidades	Pulgadas	Centro	Abscisa X	Ordenada Y
A - 144	Línea de acotación	144 x 144	128 x 128	Amarillo	0	0
L - 150	Límite de la rejilla de 150 unidades	150 x 150	133 y 1/3 x 133 y 1/3
L - 152	Límite de la rejilla de 152 unidades	152 x 152	135 y 1/9 x 135 y 1/9
B - 155,25	Borde del orillo del lino original	155,25 x 155,25	138 x 138	Azul	0	0,375
	Pared del Fondo	72 x 60	64 x 53 y 1/3	Amarillo	0	0

Desglose del centro de Las Meninas

0,375 unidades = 7,75 mm.

60 PULGADAS EN LA REJILLA DE TRABAJO

Las Coordenadas del Espejo

Como hemos ya comentado, en el estudio del espejo hay que tener en cuenta ciertos factores geométricos:

El rectángulo de trazado amarillo, que rodea el perímetro del Marco de madera del Espejo, y el rectángulo interior de trazado azul, que rodea el perímetro del Cristal del espejo, tienen como centro estas mismas coordenadas:

X = 0,15 ; Y = - 9.

Junto al lateral izquierdo del Marco de madera del Espejo se observa la sombra provocada por el efecto de la luz principal que entra por las ventanas de la derecha.
Esta aclaración gráfica no altera, en ningún caso, la posición de la Sefira nº 9, Yesod, El Fundamento:

X = 0 ; Y = - 9.

La anchura del Espejo

Y será en la misma anchura del Espejo de este lienzo donde Velázquez proponga la regia medida del Pie Real.

La anchura del Marco del Espejo mide 1 Pie Real.

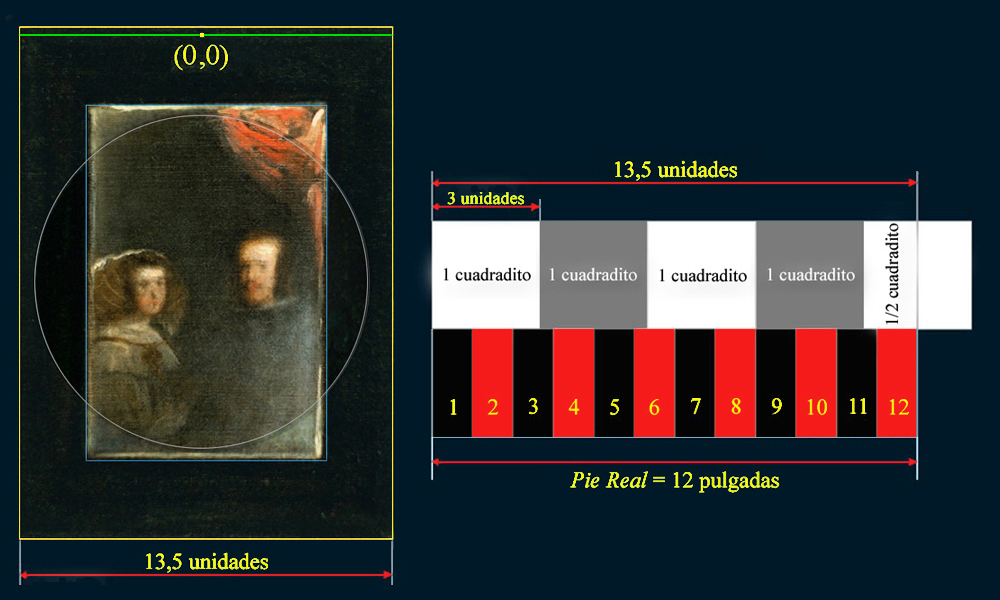La anchura del Marco del Espejo mide 13,5 unidades

Aplicación del sistema de medidas castellano:

Si una pulgada equivale a 1,125 unidades en la cuadrícula de trabajo, entonces; sólo hay que multiplicar 1,125 unidades por 12 para obtener 13,5 unidades, que es la cantidad que representa en esta misma cuadrícula 4,5 cuadraditos valiendo el Pie Real 12 pulgadas [1].

Primera conclusión:

La anchura del Marco del Espejo mide 1 Pie Real en la rejilla, que equivale a 13,5 unidades.

Segunda conclusión:

El tamaño real de la anchura del Marco del Espejo mide 1,04625 metros.

Para averiguar este segundo resultado hemos usado un coeficiente o ratio que pone de acuerdo el tamaño de los objetos pintados, que se hallen localizados en la sección del muro del fondo de Las Meninas, con la realidad.

Resultado directo:

Veamos; 13,5 unidades x 3,333333... pulgadas por unidad = 44,999999... pulgadas.

En el sistema castellano tendremos: 1,04625 metros / 0,02325 metros por pulgada = 45 pulgadas.

45 pulgadas = 3 pies y 3/4 de pie, que es lo mismo a 3 pies y 1 palmo, y que también equivalen a 5 palmos.

Esta segunda conclusión implica un razonamiento más profundo:

Primero:

El pintor Diego Velázquez midió la anchura del Marco del Espejo, que medía 45 pulgadas de ancho, y dividió esta cantidad entre 3,333333... pulgadas por unidad.

Segundo:

El pintor obtuvo directamente la medida proporcional de la anchura del Marco del Espejo:

45 pulgadas / 3,333333... pulgadas por unidad = 13,5 unidades.

Y finalmente transportó esta medida de 13,5 unidades sobre la cuadrícula de trabajo que proponemos, para así pintar, en la sección del área del muro del fondo de Las Meninas, el tamaño escalado de la anchura del Marco del Espejo.

El tamaño del Marco del Espejo

Respecto al Marco del Espejo analizaremos su tamaño real, es decir; su tamaño original antes de que fuera reducido proporcionalmente de formato y pintado en la pared del fondo de esta pintura.

Ofrecemos tanto las dimensiones en unidades, pulgadas y metros, sobre la rejilla de trabajo, como las medidas reales en pulgadas de este objeto pintado en Las Meninas en particular.

Marco del Espejo	unidades	pulgadas	metros	tamaño inicial en pulgadas
Anchura	13,5	12	0,279	13,5 x 3,333333... = 45
Altura	18,6	16 y 8/15	0,3844	18,6 x 3,333333... = 62

Las medidas del Marco del Espejo

La anchura del Marco del Espejo mide 13,5 unidades

Factorización de 3 x 3 x 3 x 5 = 135.

Los divisores del número 135 son 8:

1, 3, 5, 9, 15, 27, 45, 135.

135 ÷ 1,125 = 120; que es lo que mide en pulgadas el ancho original del lienzo de Las Meninas.

La altura del Marco del Espejo mide 18,6 unidades

Factorización de 2 x 3 x 31 = 186.

Los divisores del número 186 son 8:

1, 2, 3, 6, 31, 62, 93, 186.

186 ÷ 8 = 23,25; que es la cantidad que equivale en milímetros una pulgada castellana.

LA ALTURA					FUNDAMENTO	LA ANCHURA
Metros	Pulgadas	Unidades		Cuadrícula		Cuadrícula		Unidades	Pulgadas	Metros
0,3844	16 y 8/15	18,6	=	18,6 x 1		13,5 x 1	=	13,5	12	0,279
0,3844	16 y 8/15	18,6	=	9,3 x 2		4,5 x 3	=	13,5	12	0,279
0,3844	16 y 8/15	18,6	=	6,2 x 3		2,7 x 5	=	13,5	12	0,279
0,3844	16 y 8/15	18,6	=	3,1 x 6		1,5 x 9	=	13,5	12	0,279
0,3844	16 y 8/15	18,6	=	0,6 x 31		0,9 x 15	=	13,5	12	0,279
0,3844	16 y 8/15	18,6	=	0,3 x 62		0,5 x 27	=	13,5	12	0,279
0,3844	16 y 8/15	18,6	=	0,2 x 93		0,3 x 45	=	13,5	12	0,279
0,3844	16 y 8/15	18,6	=	0,1 x 186		0,1 x 135	=	13,5	12	0,279

Cuadrículas de Trabajo del Marco de madera del Espejo

Marco del Espejo	Metros	Pulgadas	Unidades		Unidades por pulgada		Tamaño real en pulgadas
Anchura	0,279	12	13,5	=	0,3	x	45
Altura	0,3844	16 y 8/15	18,6	=	0,3	x	62

Tamaño real del Marco de madera del Espejo

El tamaño del Cristal del Espejo

Respecto al Cristal del Espejo analizaremos también su tamaño real, es decir; su tamaño original antes de que fuera reducido proporcionalmente de formato y pintado en la pared del fondo de esta pintura.

Ofrecemos tanto las dimensiones en unidades, pulgadas y metros, sobre la rejilla de trabajo, como las medidas reales en pulgadas de este objeto pintado en Las Meninas en particular:

Cristal del Espejo	unidades	pulgadas	metros	tamaño inicial en pulgadas
Anchura	8,4	7 y 7/15	0,1736	8,4 x 3,333333... = 28
Altura	12,6	11,2	0,2604	12,6 x 3,333333... = 42

Las medidas de luces del Cristal del Espejo

La anchura del Cristal del Espejo mide 8,4 unidades

Factorización de 2 x 2 x 3 x 7 = 84.

Los divisores del número 84 son 12:

1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84.

La altura del Cristal del Espejo mide 12,6 unidades

Factorización de 2 x 3 x 3 x 7 = 126.

Los divisores del número 126 son 12:

1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126.

LA ALTURA				FUNDAMENTO	LA ANCHURA
Metros	Pulgadas	Unidades	Cuadrícula		Cuadrícula	Unidades	Pulgadas	Metros
0,2604	11,2	12,6	1 x 12,6		1 x 8,4	8,4	7 y 7/15	0,1736
0,2604	11,2	12,6	2 x 6,3		2 x 4,2	8,4	7 y 7/15	0,1736
0,2604	11,2	12,6	3 x 4,2		3 x 2,8	8,4	7 y 7/15	0,1736
0,2604	11,2	12,6	6 x 2,1		4 x 2,1	8,4	7 y 7/15	0,1736
0,2604	11,2	12,6	7 x 1,8		6 x 1,4	8,4	7 y 7/15	0,1736
0,2604	11,2	12,6	9 x 1,4		7 x 1,2	8,4	7 y 7/15	0,1736
0,2604	11,2	12,6	14 x 0,9		12 x 0,7	8,4	7 y 7/15	0,1736
0,2604	11,2	12,6	18 x 0,7		14 x 0,6	8,4	7 y 7/15	0,1736
0,2604	11,2	12,6	21 x 0,6		21 x 0,4	8,4	7 y 7/15	0,1736
0,2604	11,2	12,6	42 x 0,3		28 x 0,3	8,4	7 y 7/15	0,1736
0,2604	11,2	12,6	63 x 0,2		42 x 0,2	8,4	7 y 7/15	0,1736
0,2604	11,2	12,6	126 x 0,1		84 x 0,1	8,4	7 y 7/15	0,1736

Cuadrículas de Trabajo del Cristal del Espejo

Cristal del Espejo	Metros	Pulgadas	Unidades		Unidades por pulgada		Tamaño real en pulgadas
Anchura	0,1736	7 y 7/15	8,4	=	0,3	x	28
Altura	0,2604	11,2	12,6	=	0,3	x	42

Tamaño real del Cristal del Espejo

ESPECIFICACIONES TÉCNICAS

Poco a poco nos hemos adentrado en el estudio del eje central y vertical de Las Meninas, y ha sido menester renovar información con datos que habían quedado a medio explicar; como ha sido el caso del formato exacto del espejo con los reyes reflejados en su interior.

En una página anexa hemos confirmado el método de dimensionar el tamaño real de los objetos pintados a una distancia dada por el pintor, sólo quedaba poner a prueba esas averiguaciones y relacionarla con la zona visual más cercana al espectador de esta pintura.

El triple centro vertical de Las Meninas se explicaría del siguiente modo:

El centro geométrico del espacio de separación entre los dos grandes cuadros de la pared del fondo.

El espacio de separación entre los dos grandes cuadros, vector S, se promedia de acuerdo al eje central que pasa por el punto E

El eje central de toda la amplitud del área de esta obra de arte; siempre y cuando Las Meninas hubieran sido pensadas a partir de un cuadrado, pasa por el punto E.
Y el centro de la base esférica de la jarrita roja de Tonalá:

X = 0,3 ; Y = -38,75

La línea roja vertical pasa por el punto E, que queda representado por la coordenada [0,0],
y la base esférica de la jarrita de Tonalá tiene su centro a 0,3 unidades de esta misma vertical mencionada.

El espacio de separación entre los grandes cuadros de la pared del fondo tiene como eje intermedio la abscisa 0,3, es decir; el centro de la base esférica de la jarrita mencionada.

Hemos puesto a prueba la herramienta que en el siglo XVII se utilizaba para medir, y la aplicaremos, una vez más, para mantener el nivel de exactitud de las medidas mostradas.

La Vara Castellana, que equivale a tres pies, será la que justifique la indudable relación entre la base geométrica y la Aritmética.

	pies	pulgadas	unidades	metros
Vara	3	36	40,5	0,837

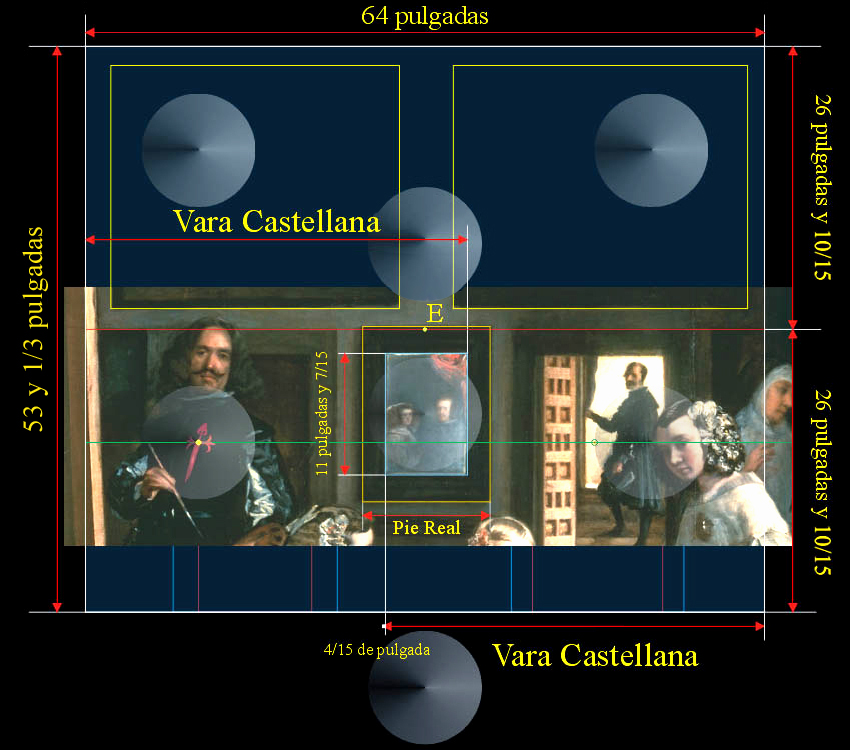El pie castellano equivale a 0,279 metros

La Vara Castellana no podía faltar a este envite de Geometría Práctica

Esta imagen anterior nos parece suficientemente aclaratoria:

La Vara Castellana mide tres pies, es decir; 0,837 metros, y, por lo que hemos investigado sobre la superficie del cuadro, no tiene aplicación práctica necesariamente, pero sí es verdad que el pintor Velázquez la usa eficazmente para situar, al menos, el canto vertical derecho del Cristal del Espejo de Las Meninas a una Vara Castellana respecto a la arista lateral izquierda de la Pared del Fondo.

Hemos detectado en el canto vertical izquierdo del Cristal del Espejo respecto la arista lateral derecha de la Pared del Fondo una variación de 4/15 de pulgada, que corresponde a 0,0062 metros, más o menos 6 milímetros.

Habría que indicar que este error, o tolerancia, es usado por el pintor con fines, tácitamente, estéticos, e impedir, de este modo, una absoluta simetría del espejo respecto a la anchura total de la pared que lo soporta.

Para que el Cristal del Espejo estuviera simétricamente centrado, respecto a ambas aristas laterales de la pared del fondo, debería tener un ancho de luces exactamente de 30 pulgadas reales, es decir; el equivalente a 9 unidades en la rejilla de trabajo.

Veamos: 30 dividido entre 3,333333... = 9; en este caso 9 unidades sería el ancho de luces del espejo.

Si la pared del fondo mide de ancho 72 unidades, la mitad de esta cifra es 36.

Si sumamos la mitad del Cristal del Espejo, es decir 9/2 = 4,5 unidades; más 36 unidades, la mitad del ancho de la pared del fondo, obtendremos exactamente 40,5 unidades.

40,5 unidades representan en nuestro plano a una Vara Castellana; y en este caso el Cristal del Espejo estaría totalmente centrado en la pared del fondo.

Conclusión:

Como hemos explicado en líneas anteriores:

En la rejilla de trabajo una pulgada castellana equivale a 1,125 unidades.

Y sabemos que la diezmillonésima parte del arco de meridiano que va del polo Norte al Ecuador, que corresponde al metro centesimal, se implantó en España por ley del 19 de julio de 1849 como nuevo patrón de medidas longitudinales.

Entonces, si la Vara Castellana mide tres pies, es decir; 0,837 metros, por tanto un Pie Real mide 0,279 metros; y, bajo estas mismas premisas, el metro centesimal equivale a 43 pulgadas y 1/93 [2].

Hablamos, pues, de la centenaria relación entre el Pie Real Castellano del rey Felipe II y el Metro francés de Napoleón Bonaparte.

Magnitud	Fecha	Divisiones	Dedos Egipcios	Milímetros	Unidades Centesimales		Centímetros	Unidades Sexagesimales
Pie Castellano	1568	12/12	14,88	279			27,9	360 x 1,125/30	=	13,5
Metro	1800	1000/1000	53,333333...	1000	1333,333333... x 1,125/15	=	100

Relación Aritmética

Y de la milenaria conexión entre la Vara de Maya del faraón Tutankhamon y el Metro francés de Napoleón Bonaparte.

Magnitud	Divisiones	Dedos Egipcios	Milímetros	Unidades Centesimales		Centímetros
Dedo Egipcio	1/28	1	18,75	25 x 1,125/15	=	1,875
Vara de Maya	28/28	28	525	700 x 1,125/15	=	52,5
Metro	1000/1000	53,333333...	1000	1333,333333... x 1,125/15	=	100

Relación Aritmética

Unidades Castellanas	División de la pulgada en 12 líneas	Pulgadas	Dedo Egipcio	Milímetros
1,125	12/12	1		23,25
0,9375	10/12	0,833333...		19,375
			1	18,75

Corolario

10/12 de pulgada castellana = 1 dedo egipcio + 0,625 milímetros.

La unidad equivale a 8/9 de pulgada

Recordamos que hemos usado tres rejillas cuadradas que difieren en seis y dos unidades, respectivamente, en el tamaño de sus respectivos lados [3].

Modelo	Cuadrículas	Anchura	*Altura*	Abscisa X	Ordenada Y
A - 144	Línea de acotación	144	144	0	0
L - 150	Límite de la rejilla de 150 unidades	150	150	0	0
L - 152	Límite de la rejilla de 152 unidades	152	152	0	0

La Geometría cuadrada de Las Meninas

Cada unidad en el plano que presentamos equivale a 8/9 de pulgada, que traducido al sistema métrico equivale a:

El Pie Real de 0,279 metros dividido entre doce es igual a 0,02325 metros la pulgada, este resultado, a su vez, lo dividimos entre 9, lo que da como resultado 0,002583... metros ó 1/9 de pulgada.

La solución de la equivalencia de 8/9 de pulgada en el sistema métrico será por tanto la multiplicación de 0,002583... metros por 8, que es igual a 0,020666... metros.

Más o menos 2 centímetros.

Si una pulgada vale 0,02325 metros y equivale a ------------------------------ 1,125 unidades.

8/9 de pulgada que es igual a 0,020666... metros equivaldrá a ------------------ X unidades.

Hagamos esta simple regla de tres:

0,020666... x 1,125 / 0,02325 = 1 unidad.

Observamos que en el primer caso tenemos una diferencia de dos unidades entre ambas rejillas, y nos estamos refiriendo a la diferencia de tamaño entre la rejilla Límite de la rejilla de 150 unidades y la otra que llamamos Límite de la rejilla de 152 unidades:

La diferencia será igual a 0,020666... metros x 2, es decir; 0,041333... metros en el formato del lado de la cuadricula.

En el caso de una diferencia de seis unidades tendremos:

0,020666666 metros x 6 = 0,124 metros.

En la siguiente tabla de medidas comparativas se muestra el procedimiento del cálculo matemático y la razón por la cual hemos dividido a la pulgada castellana en 9 partes iguales, y así poder operar con la unidad.

Unidades	División de la pulgada en 9 partes	Pulgadas	Milímetros en el sistema métrico
1,125	9/9	1	23,25
1	8/9	0,888888	20,66666...
0,875	7/9	0,777777	18,08333...
0,75	6/9	0,666666	15,5
0,625	5/9	0,555555	12,91666...
0,5	4/9	0,444444	10,33333...
0,375	3/9	0,333333	7,75
0,25	2/9	0,222222	5,166666...
0,125	1/9	0,111111	2,583333...

Tabla de equivalencia entre las unidades, la pulgada castellana y el milímetro centesimal

La pulgada dividida en nueve fracciones, que llamamos la división velazqueña, está en estrecha relación con cada una de las 12 líneas en las que se divide la pulgada castellana:

A través de las cantidades 3 y 4; números correspondientes al tamaño de los catetos del triángulo pitagórico o escuadra perfecta.

la división velazqueña	la pulgada castellana
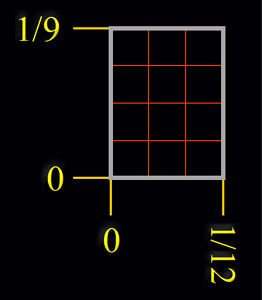1/9 = 16 puntos	1/12 = 12 puntos
4 partes x 9 = 36 partes	3 partes x 12 = 36 partes
9 fracciones	12 fracciones
1/9 ⇔ 23,25/9 = 2,583333... milímetros	1/12 ⇔ 23,25/12 = 1,9375 milímetros

Sin contrariar al viejo sistema de medición castellano, podríamos ya decir que Velázquez hace uso de la pulgada fraccionada en 9 partes para poder así representar a la unidad en sus precisas operaciones:

8/9 de pulgada equivalen a la unidad en este nuevo plano de Las Meninas.

EL CENTRO ABSOLUTO DEL LIENZO

La herramienta geométrica que denominamos Borde del orillo del lino original no es propiamente hablando una rejilla, sino que es la acotación del contorno cuadrado de 155,25 unidades, que equivale a 138 pulgadas, especifica el perímetro o borde limítrofe del lienzo de Las Meninas, a partir del orillo de su lateral derecho, antes de ser montado y clavado a su bastidor original.

Desglose de la anchura de Las Meninas

2,761583333 metros = 133,625 unidades; que equivalen a 118 pulgadas y 7/9.

Desde el centro hasta el margen derecho es igual a 69 pulgadas = 77,625 unidades.
Desde el centro hasta el margen izquierdo es igual a 49 pulgadas y 7/9 = 56 unidades.

En esta ilustración se comprueba que esta pintura fue concebida a partir de un perfecto cuadrado; y como se puede observar se deduce que la altura del lienzo original de Las Meninas medía el doble del ancho de la distancia entre el centro del espejo y el borde del orillo del lino original en el canto derecho del moderno bastidor.

El punto F es el centro de la anchura inicial del lienzo de Las Meninas

1º caso - En la nariz de la Infanta en la anchura de 2,79 metros, que equivale a 120 pulgadas
2º caso - Sobre el ojo izquierdo de la Infanta Margarita en la anchura de 2,76158333 metros

El punto F del 1º Caso es el centro inicial del lienzo de Las Meninas.

Es decir:

Horizontal : 10,125 unidades
Vertical : 0,375 unidades

notas a pie de página

1 - En la cuadrícula denominada Límite de la rejilla de 150 unidades el Pie Real equivale a 4,5 cuadraditos, y hemos dicho también; que sobre esta misma rejilla 4,5 cuadraditos es lo que mide la anchura del Marco del Espejo. En los próximos renglones analizaremos la verdadera anchura del Marco del Espejo en relación con su distancia sobre la pared del fondo.

Como demostraremos; la anchura real del Marco del Espejo equivale a 45 pulgadas. Es en este punto, entonces, donde ya deberíamos percibir la relación inmediata entre los cuadraditos de la cuadrícula Límite de la rejilla de 150 unidades y la anchura real del Marco del Espejo:

4,5 cuadraditos usados en la medición real de la anchura del Marco del Espejo equivalen a 45 pulgadas.

Podemos incorporar otro ejemplo:

Si la pared del fondo se compone de 24 cuadraditos, entonces el tamaño real de la pared del fondo será de 240 pulgadas, como así lo es.

Cierto; para llegar a la misma conclusión hay otro camino: 72 unidades x 3,333333... pulgadas por unidad = 240 pulgadas.

Todas estas cifras se pueden relacionar una con la otra, pero sabiendo que en la cuadrícula hallamos dos tipos de mediciones:

Una es la que mide en proporción a la distancia sobre la sección de la pared del fondo.
Y la otra es la que mide en unidades sobre la superficie del lienzo que cubre la cuadrícula.

Razonemos:

Medición en pulgadas sobre la sección de la pared del fondo.

Hemos dicho que el tamaño real de la pared del fondo es de 240 pulgadas que equivale a 24 cuadraditos, por lo tanto, en la rejilla Límite de la rejilla de 150 unidades la medida de una pulgada en la distancia sobre la sección de la pared del fondo equivaldrá a:

Si a 240 pulgadas le corresponden ------------------- 24 cuadraditos.

a 1 pulgada le corresponderán --------------------- X cuadraditos.

X = 1 x 24 / 240 = 0,1 de cuadradito.

Medición en unidades sobre la superficie de la cuadrícula.

La rejilla Límite de la rejilla de 150 unidades se compone de 50 cuadraditos, es decir; de 50 cuadraditos de 3 unidades cada uno.

Si a 1 cuadradito le corresponden ------------------- 3 unidades.

a 0,1 de cuadradito le corresponderá --------------------- X unidades.

X = 3 x 0,1 / 1 = 0,3 de unidad.

Luego el valor de 1 unidad en la rejilla de medición sobre la sección de la pared del fondo será:

Si a 0,3 de unidad le corresponde ------------------- 1 pulgada.

a 1 unidad le corresponderá --------------------- X pulgadas.

X = 1 x 1 / 0,3 = 3,333333... pulgadas.

Demostración:

1 pulgada en la rejilla de medición equivalen en el mundo real de la pared del fondo a:

1 pulgada = 0,3 de unidad x 3,333333... pulgadas / 1 unidad = 0,02325 metros.

Y para el caso de la anchura del del Marco del Espejo en relación con su distancia sobre la pared del fondo tendremos:

13,5 unidades x 3,333333... pulgadas por unidad = 45 pulgadas x 0,02335 metros por pulgada = 1,04625 metros.

2 - Páginas XIII y XIV - SISTEMA MÉTRICO-DECIMAL.

TABLAS QUE ESTABLECEN LA RELACION QUE EXISTE ENTRE LOS VALORES DE LAS ANTIGUAS MEDIDAS MEXICANAS Y LAS DEL NUEVO SISTEMA LEGAL, FORMADAS EN EL MINISTERIO DE FOMENTO, CONFORME A LA LEY DE 15 DE MARZO DE 1857. MÉXICO.

IMPRENTA DE J..M..ANDRADE Y F. ESCALANTE. CASA DE CADENA NUMERO 18.

PARTE SEGUNDA

MEDIDAS LINEALES

Dos siglos después de la conquista, el gobierno español remitió á México los patrones de las medidas que debían regir en el país, y entre éstas la vara que había de servir de norma para las medidas lineales. Es de creerse que se tuvo la intención que ésta fuese una copia exacta de la vara de Burgos, la que en España es la que mas generalmente se emplea; sin embargo, la diferencia que se nota entre el valor de esta medida, comparada con la vara que llegó á México, es demasiado considerable.

Císcar describe con evidente exactitud la vara de Burgos, y manifiesta todas las imperfecciones de su construcción; pero á pesar de esto, la vara de Burgos, siendo hecha de hierro y de platina el patrón original del metro, y habiendo sido rigurosamente determinadas las dilataciones de ambos metales, se ha podido establecer una comparación entre las dos medidas con una notable aproximación, y el valor de la vara de Burgos resultó ser, según unos, de metros 0,8359056936, y según otros, de metros 0,83590580, ambos valores sensiblemente iguales.

La vara mexicana, cuyo patrón se halla depositado en la oficina del Fiel-contraste de esta capital, aparece haber sido construida en Burgos el año de 1721. Es de madera, y tiene sus extremidades guarnecidas con casquillos de hierro, la tapa de uno de los cuales se ha desprendido en parte y se presta á movimientos demasiado sensibles. En varias épocas fueron nombradas comisiones con el encargo de averiguar el valor verdadero de la vara mexicana, pero sin resultados plausibles; ni podía ser de otro modo, pues si las dilataciones de los metales se sujetan á leyes fijas y bien conocidas, no hay reglas que determinen las alteraciones que sufren las maderas á consecuencia de la torsión y de los cambio higrométricos.

Entre las comisiones mencionadas, la última, comparando á la simple vista, y sin mas advertencias, un metro modelo de acero con la vara del Fiel-contraste, creyó adivinar que ésta equivalía á metros 0,83731, cuyo resultado dista notablemente del valor de la vara de Burgos.

Si estos trabajos han sido infructuosos, el que todavía merece mas fe, es el que se efectuó por el año de 1838, cuando se trató de una cesión de terrenos que el gobierno de México se proponía hacer á ciertos acreedores; pues á mas de atenderse á la temperatura, se midieron con un compas de vara (Beam Compass), construido por W. Cary, dividido en pulgadas inglesas y centésimos de líneas, que podían ser apreciados por medio de nonios, las cuatro aristas de la vara del Fiel-contraste, y un término medio de estos resultados dió á conocer que la vara corresponde aproximadamente á 838 milímetros, cuyo valor legalmente aprobado se adoptó también para construir las tablas que se ponen al fin de esta Introducción.